 Coba Anda sebutkan 2 rasi bintang yang terlihat pada gambar di atas.
Coba Anda sebutkan 2 rasi bintang yang terlihat pada gambar di atas.Jawaban silakan Anda disampaikan lewat kolom komentar.
Selamat mencoba.
 Coba Anda sebutkan 2 rasi bintang yang terlihat pada gambar di atas.
Coba Anda sebutkan 2 rasi bintang yang terlihat pada gambar di atas.| No. | B | V |
| 1 | 8,52 | 8,82 |
| 2 | 7,45 | 7,25 |
| 3 | 7,45 | 6,35 |
| Nomor bintang | B | V | B - V |
| 1. | 8,52 | 8,82 | -0,30 |
| 2. | 7,45 | 7,25 | 0,20 |
| 3. | 7,45 | 6,35 | 1,10 |
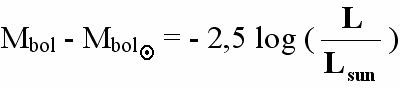 Dengan Mbol = magnitudo mutlak bolometrik bintang
Dengan Mbol = magnitudo mutlak bolometrik bintangmv – mbol = BC
Mv – Mbol = BC
 Untuk Matahari, magnitudo bolometriknya (mbol¤) = -26,83, magnitudo mutlak bolometriknya adalah Mbol¤ = 4,74 dan koreksi bolometriknya BC = 0,08. Berikut disajikan tabel temperatur efektif dan koreksi bolometrik untuk bintang-bintang deret utama dan bintang maharaksasa.
Untuk Matahari, magnitudo bolometriknya (mbol¤) = -26,83, magnitudo mutlak bolometriknya adalah Mbol¤ = 4,74 dan koreksi bolometriknya BC = 0,08. Berikut disajikan tabel temperatur efektif dan koreksi bolometrik untuk bintang-bintang deret utama dan bintang maharaksasa.| B - V | Bintang deret utama | Bintang maharaksasa | ||
| Tef | BC | Tef | BC | |
| - 0,25 | 24500 | 2,30 | 26000 | 2,20 |
| - 0,23 | 21000 | 2,15 | 23500 | 2,05 |
| - 0,20 | 17700 | 1,80 | 19100 | 1,72 |
| - 0,15 | 14000 | 1,20 | 14500 | 1,12 |
| - 0,10 | 11800 | 0,61 | 12700 | 0,53 |
| - 0,01 | 10500 | 0,33 | 11000 | 0,14 |
| 0,00 | 9480 | 0,15 | 9800 | - 0,01 |
| 0,10 | 8530 | 0,04 | 8500 | - 0,09 |
| 0,20 | 7910 | 0 | 7440 | - 0,10 |
| 0,30 | 7450 | 0 | 6800 | - 0,10 |
| 0,40 | 6800 | 0 | 6370 | - 0,09 |
| 0,50 | 6310 | 0,03 | 6020 | - 0,07 |
| 0,60 | 5910 | 0,07 | 5800 | - 0,003 |
| 0,70 | 5540 | 0,12 | 546 | 0,003 |
| 0,80 | 5330 | 0,19 | 5200 | 0,10 |
| 0,90 | 5090 | 0,28 | 4980 | 0,19 |
| 1,00 | 4840 | 0,40 | 4770 | 0,30 |
| 1,20 | 4350 | 0,75 | 4400 | 0,59 |
| Jenis bintang | MV | Jumlah (%) |
| a | 1 | 20 |
| b | 4 | 50 |
| c | 6 | 30 |
Fotometri adalah bagian dari astrofisika yang mempelajari kuantitas, kualitas dan arah pancaran radiasi elektromagnetik dari benda langit. Penggunaan kata ‘foto’ yang berarti ‘cahaya’ disebabkan pada awalnya pengamatan benda langit hanya terbatas pada panjang gelombang visual/optik.
Fotometri didasarkan pada pemahaman atas hukum pancaran (radiation law). Kita menghipotesakan bahwa benda langit diangggap memiliki sifat sebuah benda hitam (black body).
Sifat benda hitam antara lain :
1) pada kesetimbangan termal, temperatur benda hanya ditentukan oleh jumlah energi yang diserapnya per detik;
2) benda hitam tidak memancarkan radiasi pada seluruh gelombang elektromagnetik dengan intensitas yang sama (ada yang dominan meradiasikan gelombang elektromagnetik pada daerah biru dengan intensitas yang lebih besar dibandingkan gelombang elektromagnetik pada panjang gelombang lainnya. Konsekuensinya, benda tersebut akan nampak biru).
Panjang gelombang yang dipancarkan dengan intensitas maksimum (λmaks) oleh sebuah benda hitam dengan temperatur T Kelvin adalah :
λmaks = 0,2898/ T .......................... (pers. 1)
(λmaks dinyatakan dalam cm dan T dalam Kelvin)
Persamaan di atas disebut dengan Hukum Wien.
Contoh penggunaan hukum Wien : (Warning : Yang perlu diperhatikan bahwa λmaks bukan berarti panjang gelombang maksimum tetapi panjang gelombang yang dipancarkan dengan intensitas maksimum)
(Warning : Yang perlu diperhatikan bahwa λmaks bukan berarti panjang gelombang maksimum tetapi panjang gelombang yang dipancarkan dengan intensitas maksimum)Jumlah energi per satuan waktu yang dipancarkan sebuah benda hitam per satuan luas permukaan pemancar (benda hitam) disebut fluks energi yang dipancarkan. Besarnya fluks energi yang dipancarkan sebuah benda hitam (F) dengan temperatur T Kelvin adalah :
F = σT4 .......................... (pers. 2)
(σ : konstanta Stefan-Boltzman : 5,67 x 10^-8 Watt/m2K4)
Sedangkan total energi per waktu / daya yang dipancarkan sebuah benda hitam dengan luas permukaan pemancar A dan temperatur T Kelvin disebut dengan Luminositas. Besarnya luminositas (L) dihitung dengan persamaan :
L = A σT4 .......................... (pers. 3)
Untuk bintang, bintang dianggap berbentuk bola sempurna sehingga luas pemancar radiasinya (A) adalah 4πR2 ; dengan R menyatakan radius bintang. Jadi, luminositas bintang (L) adalah :
L = 4πR2 σT4 .......................... (pers. 4)
Benda hitam memancarkan radiasinya ke segala arah. Kita bisa menganggap pancaran radiasi tersebut menembus permukaan berbentuk bola dengan radius d dengan fluks energi yang sama, yaitu E. Besarnya E :
E = L/(4πd2) .......................... (pers. 5)
Fluks energi inilah yang diterima oleh pengamat dari bintang yang berada pada jarak d dari pengamat. Oleh karena itu, fluks energi ini sering disebut fluks energi yang diterima pengamat. (Warning : bedakan antara besaran E dan F).
 Latihan:
Latihan: Ian Ridpath has been adding to his impressive list of publications with the recently updated fourth edition of "Stars and Planets". Or, consider its more accurate and complete title "Princeton Field Guides Stars & Planets - The Most Complete Guide to the Stars, Planets, Galaxies and the Solar System". The title's quite a mouthful, but the book lives up to the billing. Within it, Ian Ridpath's texts and Wil Tirion's illustrations cover all that would interest an active, backyard astronomer.
Ian Ridpath has been adding to his impressive list of publications with the recently updated fourth edition of "Stars and Planets". Or, consider its more accurate and complete title "Princeton Field Guides Stars & Planets - The Most Complete Guide to the Stars, Planets, Galaxies and the Solar System". The title's quite a mouthful, but the book lives up to the billing. Within it, Ian Ridpath's texts and Wil Tirion's illustrations cover all that would interest an active, backyard astronomer.Being the fourth edition, this review should assess changes from the book's predecessor. Lacking the third edition means I'm considering the book in isolation.
This book has two parts. The first includes star charts; four per month, with the northern latitude facing south and then north and the same for the southern latitude. The charts show about 5000 separate stars, all being a white dot on a pale blue background with black lettering. After this inclusion, there's notes on each of the 88 constellations. Again, star charts accompany each. To further entice the reader, nearly each constellation description has a wonderful, colour photograph of a particularly rewarding view, usually as seen from the National Optical Astronomy Observatory (NOAO) in
However, as much as the NOAO facility is for the big league, this book stays true to being a guide for the amateur. As such, nearly all comments on viewing, and there are many, relate to either binoculars or small to mid-size home telescopes.
The second part of the book starts off with a look into the life cycle of stars and the particular and useful intricacies of the electromagnetic spectrum. Then, it proceeds to describe viewing pleasures on a planet by planet meander through our solar system. Further, twelve full page maps completely identify features shown on the Moon's near side. Again, the perspective is for that of a person using amateur level equipment. To help the reader along, the book concludes with a short discussion on choosing binoculars and telescopes.
Being a field guide, this book is of smaller stature than most. Yet, it still won't fit easily into most pant pockets. However, it would be a great asset to have on hand when deciding how to coordinate a star party or optimize personal evening viewing. And, though not stated in the title, it is for observers, so there's not a great depth of detail on why or what-for. Thus, for observers, it is of a just the right stature.
Though I'm not in a position to asses the title's proclamation of being the most complete guide, I will say that it is the best one that I've read. With Ian Ridpath's text and Wil Tirion's illustrations, the "Princeton Field Guides Stars & Planets" is a wonderful guide to the stars, planets, galaxies and our own solar system. It will help in getting that illusive target into the finder and onto the eagerly awaiting eye.
(Written by Mark Mortimer)
Buku ini cocok digunakan khususnya oleh para astronom amatir, yang ingin mendapatkan panduan praktis dalam melakukan pengamatan. Buku ini menyertakan peta bintang, peta permukaan Bulan dan overview mengenai gelombang elektromagnetik dan tahapan evolusi bintang. Jika Anda tertarik membeli buku ini secara online, silakan klik link ini.
This blog is intended for students who want to participate in astronomy competitions and olympiads (OSN, IAO, IOAA, APAO). Tutors and teachers can use this blog as a teaching resource. Amateur astronomers can find this blog useful,too. Its content varies from problem-set, course slide, try out, news, textbook recommendation, astronomy software review, trivia, video, and many more.