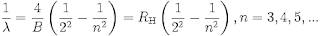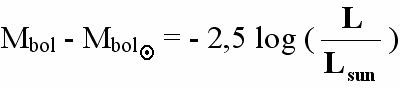Soal - Soal Latihan

Di bawah ini ada beberapa soal latihan yang dapat Anda manfaatkan untuk bahan latihan. Selamat belajar.

=========================================================

1.The following statements are true or false:

(a) Of all the natural satellites in the Solar System only the Moon always turns the same face towards its primary.

(b) The mass of a planet in the Solar System can be determined only if it possesses one or more satellites.

(c) The planet with the largest apparent angular diameter when nearest the Earth is Venus.

(d) Pluto is the planet farthest from the Sun.

(e) A lunar eclipse may occur if the Moon is new.

2. Calculate the mean density of Jupiter from the following data, assuming the orbits of Earth and Jupiter to be circular and coplanar:

· Angular semi-diameter of Jupiter at opposition = 21”,8

· Orbital radius of Jupiter = 5,2 A.U.

· Mass of Jupiter/mass of Earth = 318

· Mean density of Earth = 5,5 kg/m^-3

· Sun’s horizontal parallax = 8”,8

3. The two components of a binary star are approximately equal brightness. Their maximum separation is 1”,3 and the period is 50,2 years. The composite spectrum shows double lines with a maximum separation of 0,18 Angstrom at 5000 Angstrom. Assuming that the plane of the orbit contains the line of sight, calculate (i) the total mass of the system in the terms of the solar mass, (ii) the parallax of the system.

===================================================

(sumber : Astronomy, The Structure Of Universe).

Dasar - Dasar Spektroskopi Bintang

Spektroskopi adalah suatu cabang ilmu dalam astronomi yang mempelajari spektrum benda langit. Dari spektrum suatu benda langit dapat kita peroleh informasi mengenai temperatur, kandungan/ komponen zat penyusunnya, kecepatan geraknya, dll. Oleh sebab itu, spektroskopi merupakan salah satu ilmu dasar dalam astronomi. Spektrum sebuah bintang diperoleh dengan menggunakan alat yang disebut spektrograf.

Gambar 1. Spektrum

Gambar 2. Cara kerja spektrograf

Salah satu landasan spektroskopi adalah Hukum Kirchoff (1859):

1. Bila suatu benda cair atau gas bertekanan tinggi dipijarkan, benda tadi akan memancarkan energi dengan spektrum pada semua panjang gelombang
2. Gas bertekanan rendah bila dipijarkan akan memancarkan energi hanya pada warna, atau panjang gelombang tertentu saja. Spektrum yang diperoleh berupa garis-garis terang yang disebut garis pancaran atau garis emisi. Letak setiap garis atau panjang gelombang garis tersebut merupakan ciri gas yang memancarkannya.
3. Bila seberkas cahaya putih dengan spektrum kontinu dilewatkan melalui gas yang dingin dan renggang (bertekanan rendah), gas tersebut tersebut akan menyerap cahaya tersebut pada warna atau panjang gelombang tertentu. Akibatnya akan diperoleh spektrum kontinu yang berasal dari cahaya putih yang dilewatkan diselang-seling garis gelap yang disebut garis serapan atau garis absorpsi.

Gambar 3 & 4. Perbedaan spektrum kontinu, absorpsi dan emisi

Deret Balmer
Ilmuwan Swiss yang bernama Balmer merumuskan suatu persamaan deret untuk memprediksi panjang gelombang dari garis serapan yang dihasilkan gas hidrogen. Persamaan terebut dikenal dengan deret Balmer.

dengan : λ: panjang gelombang serapan (cm)
R_H : tetapan Rydberg (= 109678)

Gambar 5 : Spektrum emisi hidrogen yang menampilkan 4 garis spektrum pertama dalam deret Balmer

Teori Kuantum Planck

Planck mempostulatkan bahwa cahaya diradiasikan dalam bentuk paket - paket energi kecil, yang disebut kuantum. Teori inilah yang mendasari terciptanya bidang baru dalam dunia fisika, yaitu fisika kuantum.

Planck mengatakan bahwa energi dari tiap foton

E_o = h. f = hc//λ

h : tetapan Planck (h = 6,63 x 10^-34 J.s)
f : frekuensi dari foton
c = kecepatan cahaya (= 3.10^5 km/s)
λ = panjang gelombang foton

Pembentukan spektrum Bintang
Pola spektrum bintang umumnya berbeda-beda, pada tahun 1863 seorang astronom bernama Angelo Secchi mengelompokan spektrum bintang dalam 4 golongan berdasarkan kemiripan susunan garis spektrumnya.

Miss A. Maury dari Harvard Observatory menemukan bahwa klasifikasi Secchi dapat diurutkan secara kesinambungan hingga spektrum suatu bintang dengan bintang urutan sebelumnya tidak berbeda banyak. Klasifikasi yang dibuat oleh Miss Maury selanjutnya diperbaiki kembali oleh Miss Annie J. Cannon. Hingga sekarang klasifikasi Miss Cannon ini digunakan.

Tabel 1 : Rangkuman klasifikasi bintang yang saat ini umum digunakan (sering digunakan ungkapan : Oh Be A Fine Girl (or Guy), Kiss Me) untuk mengingat urutan klasifikasi kelas spektrum bintang. (klik gambar untuk tampilan lebih jelas!).

Subkelas spektrum
Klasifikasi spektrum bintang O, B, A, F, G, K, M masih dibagi lagi dalam subkelas, yaitu
B0, B1, B2, B3, . . . . . . . . ., B9
A0, A1, A2, A3, . . . . . . . . ., A9
F0, F1, F2, F3, . . . . . . . . . ., F9

Semakin besar angka yang menyatakan menunjukkan suhu bintang semakin rendah pula. Pengunaan subkelas ini dimaksudkan agar pengklasifikasian spektrum bintang menjadi lebih spesifik sehingga lebih jelas dan tepat.
(untuk informasi lebih lanjut tentang kelas spektrum bintang di sini.)

Gambar 6. Spektrum bintang dari berbagai kelas spektrum

M-K Kelas (Kelas Luminositas Bintang)
Bintang dalam kelas spektrum tertentu ternyata dapat mempunyai luminositas yang berbeda. Pada tahun 1913 Adam dan Kohlscutter di Observatorium Mount Wilson menunjukkan ketebalan beberapa garis spektrum dapat digunakan untuk menentukan luminositas bintang.
Berdasarkan kenyataan ini pada tahun 1943 Morgan dan Keenan dari Observatorium Yerkes membagi bintang dalam kelas luminositas, yaitu :

Kelas 1a	Maharaksasa yang sangat terang
Kelas 1b	Maharaksasa yang kurang terang
Kelas II	Raksasa yang terang
Kelas III	Raksasa
Kelas IV	Subraksasa
Kelas V	Bintang deret utama

Tabel 2. Kelas Luminositas Morgan Keenan

Kelas Luminositas Bintang dari Morgan-Keenan (MK) digambarkan dalam diagram Hertzprung-Russell (diagram H-R) di bawah ini.

Gambar 7. Kelas Luminositas dalam diagram H-R

Klasifikasi spektrum bintang sekarang ini merupakan penggabungan dari kelas spektrum dan kelas luminositas.

Contoh :
- G2 V : Bintang deret utama kelas spektrum G2
- G2 Ia : Bintang maharaksasa yang sangat terang kelas spektrum G2
- B5 III : Bintang raksasa kelas spektrum B5
- B5 IV : Bintang subraksasa kelas spektrum B5

Gerak Bintang
Bintang tidak diam, tapi bergerak di ruang angkasa. Pergerakan bintang ini sangat sukar diikuti karena jaraknya yang sangat jauh, sehingga kita melihat bintang seolah-olah tetap diam pada tempatnya sejak dulu hingga sekarang

Laju perubahan sudut letak suatu bintang disebut gerak sejati (proper motion). Gerak sejati bisanya diberi simbol dengan μ dan dinyatakan dalam detik busur pertahun. Bintang yang gerak sejatinya terbesar adalah bintang Barnard dengan μ = 10”,25 per tahun (dalam waktu 180 tahun bintang ini hanya bergeser selebar bulan purnama).

Gambar 8. Kecepatan bintang

Hubungan antara kecepatan tangensial (Vt) dan gerak sejati (μ):

Vt = 4,74 μ d

dengan :
Vt = kecepatan tangensial bintang (dalam km/s)
μ = laju gerak diri / proper motion (dalam “/ tahun )
d = jarak bintang (dalam parsec)

atau persamaan diatas dapat diubah ke dalam bentuk :

Vt = 4,74 μ/p

dengan p adalah sudut paralaks bintang (dalam detik busur).

Dalam pengukuran gerak sejati yang diukur bukan hanya besarnya tetapi juga ditentukan arahnya.

Gambar 9. Gerak sejati bintang

Persamaan-persamaan yang dapat digunakan untuk memperoleh nilai gerak sejati bintang:

μ_α cos δ = μ sin θ
μ_δ = μ cos θ

dengan :
μ_α = komponen pada arah α (asensiorekta)
μ_δ = komponen pada arah δ (deklinasi)
μ_α dan μ_δ dapat diukur --> μ dan θ dapat ditentukan.

Selain gerak sejati, informasi tentang gerak bintang diperoleh dari pengukuran kecepatan radial, yaitu komponen kecepatan bintang yang searah dengan garis pandang.
Kecepatan radial bintang dapat diukur dari efek Dopplernya pada garis spektrum dengan menggunakan rumus (untuk Vr mendekati c):

Jika Vr jauh lebih kecil dibandingkan kecepatan cahaya (c), maka:

Δλ/λ_o = Vr/c

dengan :
Δλ = selisih antara λ diam (λ_o) dengan λ yang teramati pada bintang. (dalam Å atau nm)
λ_o = panjang gelombang diam (dalam Å atau nm)
V_r = kecepatan radial (dalam km/s)
c = kecepatan cahaya (300.000 km/s )

Gambar 10. Red shift and blue shift

Karena Vt dan Vr sudah dapat kita tentukan dari rumus-rumus yang sudah dibahas tadi, kita bisa menghitung kecepatan linier bintang (kecepatan gerak bintang sebenarnya di ruang angkasa), yaitu :

V² = (V_t)² + (V_r)²

Contoh :
Garis spektrum suatu elemen yang panjang gelombang normalnya adalah 5000 Å diamati pada spektrum bintang berada pada panjang gelombang 5001 Å. Seberapa besarkah kecepatan pergerakan bintang tersebut ? Apakah bintang tersebut mendekati atau menjauhi Bumi ?
(Jawab : 60 km/s, MENJAUHI Bumi)

Sumber referensi:

1. Slide kuliah Astrofisika I, oleh Dr. Djoni N. Dawanas
2. Wikipedia
3. Gambar-gambar diperoleh dari sumber-sumber terpisah dari internet

Untuk referensi lainnya, silakan kunjungi:
1. Spectroscopy
2. Astronomynotes.com

Selamat belajar

Penelitian terkini tentang supermasif black hole di pusat Bimasakti

(Area pusat galaksi Bima Sakti. Kredit : ESO)

Setelah melakukan studi panjang selama 16 tahun menggunakan teleskop milik ESO, tim astronom dari Jerman berhasil memperlihatkan kondisi paling detil yang pernah ada dari area di sekitar jantung galaksi Bima Sakti - tempat diperkirakan adanya sebuah lubang hitam supermasif (super massive black hole). Penelitian ini mengungkap rahasia yang tersimpan di area tersebut melalui pemetaan orbit 28 bintang. Bahkan satu bintang di antaranya telah berhasil melakukan putaran penuh mengelilingi lubang hitam.

Pengamatan gerak 28 bintang yang mengorbit area pusat galaksi Bima Sakti, menunjukkan keberadaan lubang hitam supermasif Sagittarius A (atau dikenal sebagai bintang Sagittarius A). Berbagai informasi termasuk bentuk istimewa bintang-bintang tersebut dan juga lubang hitam yang mengikat bintang-bintang tersebut berhasil dikuak.

Pusat galaksi merupakan laboratorium yang unik dimana kita bisa belajar proses-proses dasar gravitasi yang besar dan kuat, serta dinamika dan pembentukan bintang yang memiliki keterkaitan yang sangat besar dengan inti galaksi. Di sinilah pabrik kelahiran bintang dan tempat berlabuh sang monster menakutkan, lubang hitam supermasif. Di area ini jugalah kita bisa mempelajari lubang hitam dengan lebih mendetil.

Tapi untuk mengamati area ini tidaklah mudah. Pengamatan dalam panjang gelombang tampak terhalangi oleh debu antar bintang yang mengisi galaksi. Kemampuan teknologi menjadi tantangan untuk dapat mengintip apa yang terjadi di sana. Untuk itu, digunakanlah panjang gelombang infra merah untuk menembus blokade debu antar bintang tersebut. Bintang-bintang di area pusat galaksi kemudian dijadikan partikel penguji untuk mengungkap apa yang ada di sana. Bintang-bintang itu diamati geraknya selama mengorbit Sagittarius A.

Hasil yang diperoleh sangat berguna untuk memahami lubang hitam itu sendiri contohnya dalam hal massa dan jarak dan tampaknya 95% massa yang mempengaruhi gerak bintang tersebut adalah lubang hitam. Oleh karena itu, kecil kemungkinan penyebabnya adalah karena materi kelam lain. Tak pelak, hasil ini menjadi bukti empirik keberadaan lubang hitam supermasif, yang diperlihatkan oleh bintang yang mengorbit pusat galaksi. Dalam pengamatan, diketahui adanya konsentrasi massa yang besar sekitar 4 juta massa Matahari yang diyakini sebagai lubang hitam yang berada pada jarak 27000 tahun cahaya.

Dari ke-28 bintang yang diamati, 6 di antaranya mengorbit lubang hitam dalam sebuah piringan dan bintang-bintang pada area paling dalam memiliki orbit acak. Bintang S2 menjadi satu-satunya bintang yang berhasil mengelilingi pusat Bima Sakti periode 16 tahun tersebut.

Untuk membangun citra jantung Bima Sakti dan menghitung orbit bintang individu, tim ini mempelajari bintang-bintang tersebut selama 16 tahun, dimulai pada tahun 1992 menggunakan kamera SHARP yang dipasang di New Technology Telescope 3,5 meter milik ESO di Observatorium La Silla, Chille. Observasi lainnya dibuat pada tahun 2002 dengan 2 instrumen yang ada di Very Large Telescope (VLT).

Walau penelitian ini berhasil membuka lembaran baru bagi pembelajaran lubang hitam dan kondisi area pusat galaksi dalam tingkat akurasi yang tinggi, namun masih banyak misteri yang belum terkuak di sana. Apalagi bintang-bintang tersebut juga masih sangat muda untuk melakukan perjalanan jauh. Diduga, bintang-bintang ini terbentuk pada orbitnya saat ini dibawah pengaruh gaya pasang surut lubang hitam.

Di masa depan, berbagai rancangan penelitian lanjutan akan dilakukan untuk mengintip monster di jantung Bima Sakti itu. Salah satunya dengan menggunakan teknologi dengan resolusi sudut (angular resolution) yang lebih tinggi.

Sumber : ESO

Cited with necessary change from : Langit Selatan - Situs Astronomi Indonesia

Astronomers 'Time Travel' to 16th Century Supernova

On November 11, 1572 Danish astronomer Tycho Brahe and other skywatchers observed what they thought was a new star. A bright object appeared in the constellation Cassiopeia, outshining even Venus, and it stayed there for several months until it faded from view. What Brahe actually saw was a supernova, a rare event where the violent death of a star sends out an extremely bright outburst of light and energy. The remains of this event can still be seen today as Tycho’s supernova remnant. Recently, a group of astronomers used the Subaru Telescope to attempt a type of time travel by observing the same light that Brahe saw back in the 16th century. They looked at 'light echoes' from the event in an effort to learn more about the ancient supernova.

A ‘light echo’ is light from the original supernova event that bounces off dust particles in surrounding interstellar clouds and reaches Earth many years after the direct light passes by; in this case, 436 years ago. This same team used similar methods to uncover the origin of supernova remnant Cassiopeia A in 2007. Lead project astronomer at Subaru, Dr. Tomonori Usuda, said “using light echoes in supernova remnants is time-traveling in a way, in that it allows us to go back hundreds of years to observe the first light from a supernova event. We got to relive a significant historical moment and see it as famed astronomer Tycho Brahe did hundreds of years ago. More importantly, we get to see how a supernova in our own galaxy behaves from its origin.”

The view of the light echoes from Tycho’s supernova. Credit: Subaru Telescope

On September 24, 2008, using the Faint Object Camera and Spectrograph (FOCAS) instrument at Subaru, astronomers looked at the signatures of the light echoes to see the spectra that were present when Supernova 1572 exploded. They were able to obtain information about the nature of the original blast, and determine its origin and exact type, and relate that information to what we see from its remnant today. They also studied the explosion mechanism. What they discovered is that Supernova 1572 was very typical of a Type Ia supernova. In comparing this supernova with other Type Ia supernovae outside our galaxy, they were able to show that Tycho's supernova belongs to the majority class of Normal Type Ia, and, therefore, is now the first confirmed and precisely classified supernova in our galaxy. This finding is significant because Type Ia supernovae are the primary source of heavy elements in the Universe, and play an important role as cosmological distance indicators, serving as ‘standard candles’ because the level of the luminosity is always the same for this type of supernova. For Type Ia supernovae, a white dwarf star in a close binary system is the typical source, and as the gas of the companion star accumulates onto the white dwarf, the white dwarf is progressively compressed, and eventually sets off a runaway nuclear reaction inside that eventually leads to a cataclysmic supernova outburst. However, as Type Ia supernovae with luminosity brighter/fainter than standard ones have been reported recently, the understanding of the supernova outburst mechanism has come under debate. In order to explain the diversity of the Type Ia supernovae, the Subaru team studied the outburst mechanisms in detail. This observational study at Subaru established how light echoes can be used in a spectroscopic manner to study supernovae outburst that occurred hundreds of years ago. The light echoes, when observed at different position angles from the source, enabled the team to look at the supernova in a three dimensional view. This study indicated Tycho's supernova was an aspherical/nonsymmetrical explostion. For the future, this 3D aspect will accelerate the study of the outburst mechanism of supernova based on their spatial structure, which, to date, has been impossible with distant supernovae in galaxies outside the Milky Way.

The results of this study appear in the 4 December 2008 issue of the science journal Nature.

Source: Subaru Telescope

Cited from : universe today by Nancy Atkinson

Animasi : Pengaruh Lintang Terhadap Bola Langit (Celestial Sphere)

Di bawah ini ditampilkan dua buah animasi (.gif dan flash) tentang pengaruh lintang terhadap bola langit. Pengamat pada lintang yang berbeda akan mengamati bintang terbit dan terbenam pada arah yang berbeda. Gerak edar harian nya juga berbeda. Hal ini menyebabkan ada bintang - bintang tertentu tidak pernah terbit atau tidak pernah terbenam (meskipun tidak terlihat saat siang hari). Bintang-bintang tersebut dikenal dengan nama bintang sirkumpolar.

Flash animation of Orion star trails at different latitudes

(sumber : www.astronomynotes.com)

Mengenal Objek Langit : Horsehead Nebula

One of the most identifiable nebulae in the sky, the Horsehead Nebula in Orion, is part of a large, dark, molecular cloud. Also known as Barnard 33, the unusual shape was first discovered on a photographic plate in the late 1800s. The red glow originates from hydrogen gas predominantly behind the nebula, ionized by the nearby bright star Sigma Orionis. A blue reflection nebula surrounds the bright star at the lower left. The darkness of the Horsehead is caused mostly by thick dust, although the lower part of the Horsehead's neck casts a shadow to the left. Streams of gas leaving the nebula are funneled by a strong magnetic field. Bright spots in the Horsehead Nebula's base are young stars just in the process of forming. Light takes about 1500 years to reach us from the Horsehead Nebula. The above image was taken earlier this month with a 0.6-meter telescope at the Mt. Lemmon SkyCenter in Arizona, USA.

Source : Astronomy Picture of the Day

Trivia : Coba sebutkan nomor NGC dari objek di atas? Apakah objek termasuk muncul di katalog Messier? Jika ya, coba sebutkan nomor katalognya?

Selamat mencoba. Jawaban bisa disampaikan lewat kolom komentar.
Pembaca lain juga boleh mengomentari jawaban pembaca lain sehingga bisa saling mengkoreksi atau menambahkan.

Menghitung Satuan Astronomi (Astronomical Unit)

Pendahuluan
Mungkin Anda pernah mendengar istilah AU. AU adalah singkatan dari Astronomical Unit.

Satu AU sama dengan jarak RATA-RATA Matahari ke Bumi

Nilai eksak AU yang saat ini diterima adalah 149.597.870.691 ± 30 meter (sekitar 150 juta kilometer atau 93 juta mil). Untuk keperluan perhitungan sehari-hari sering diambil 1,496 x 10⁸ km.

Satuan AU umumnya digunakan untuk menyatakan jarak benda-benda yang ada di tata surya. Alasannya adalah agar jarak benda-benda di tata surya (planet, asteoroid, dll) mudah dibandingkan dengan jarak Matahari-Bumi. Misalkan, planet Jupiter dikatakan berjarak 5,2 AU dari Matahari berarti jarak Jupiter-Matahari 5,2 kali jarak Bumi-Matahari.

Bagaimana menghitung AU?
Sebelum kita mulai membahas bagaimana para ahli menghitung besarnya satu AU, Anda sebaiknya memahami Hukum Kepler, khususnya Hukum Kepler ketiga.

Hukum ini menyatakan bahwa perbandingan pangkat tiga jarak suatu objek terhadap kuadrat periode revolusinya adaah konstan jika mengorbit objek yang sama (misalnya, semua planet memiliki nilai konstanta yang sama karena sama-sama mengitari Matahari tetapi Bulan tidak mempunyai nilai konstanta yang sama dengan planet karena Bulan mengorbit Bumi, bukan Matahari). Jika dinyatakan dalam bentuk persamaan, Hukum Ketiga Kepler berbentuk:

(a³/P²)₁ = (a³/P²)₂ = konstan

dengan : a = jarak objek dan P = periode orbit.

Sebenarnya banyak cara untuk menentukan jarak Bumi-Matahari. Salah satu teknik yang paling modern yang cukup teliti adalah dengan menggunakan radar.

Pengamatan dengan radar ini pertama kali dilakukan oleh Lincoln Laboratory, Massachusetts Institute of Technology pada tahun 1958 dengan mengirim gelombang radar berfrekuensi 440 Megahertz ke planet Venus.

Untuk penentuan ini diandaikan orbit Bumi dan Venus berbentuk lingkaran. Asumsi ini hanya mengurangi seidkit akurasi perhitungan karena orbit Venus memang hampir berupa lingkaran sempurna (eksentrisitas orbit Venus = 0,00677323).

Dari pengamatan, diketahui bahwa periode orbit Bumi adalah,

P_B = 365,25 hari

Periode orbit Venus adalah,

P_V = 224,7 hari

Dari hukum Kepler ke-3 (a³ ~ P²)

a_V/a_B = (P_V/P_B)^2/3

Dari data di atas :

a_V/a_B = (224,7/365,25)2/3 = 0,72

atau, a_V = 0,72 a_B

Ilustrasi perhitungan ini ditunjukkan dalam gambar di bawah ini:
Dengan menggunakan aturan cosinus:
Lalu, subtistusikan : a_V = 0,72 a_B ke dalam persamaan di atas dan akan diperoleh:
Nilai d dapat ditentukan dengan radar. Gelombang radar dipancarkan dari Bumi dan ditangkap sinyal pantulannya. Selang waktu kedua sinyal (sinyal utama dan sinyal pantulan) dapat digunakan sebagai skala jarak. Persamaan yang digunakan adalah:

t = 2d c

dengan :

• d = jarak antara objek pemancar sinyal (Bumi) dan objek pemantul sinyal (Venus) (diambil pada saat jarak terdekat Bumi-Venus)
• t = waktu yang ditempuh oleh gelombang radar Bumi- Venus- Bumi
• c = kecepatan gelombang elektromagnetik (cahaya, gelombang radar, dll) = 299.792.458 m/s

Nilai α juga dapat diamati dari Bumi karena α menyatakan jarak sudut (sudut pisah) antara Venus dan Matahari saat teramati dari Bumi (jarak sudut adalah jarak antara dua objek dinyatakan dalam satuan sudut). Nilai α tergantung pada posisi Bumi-Venus pada saat pengukuran.

Dengan memasukan harga d dan hasil pengamatan, diperoleh,

a_B = 1,496 x 10¹³ cm = 1 AU

Beberapa pendekatan yang digunakan dalam perhitungan ini adalah:

1. Orbit Bumi dan orbit Venus mengedari Matahari tidak berupa lingkaran sempurna, tapi berupa elips dengan eksentrisitasnya sangat kecil (eksentrisitas orbit Venus = 0,00677323). Jadi, orbit Bumi dan orbit Venus praktis dapat dianggap berupa lingkaran.
2. Selain itu juga bidang orbit Venus tidak sebidang dengan bidang orbit Bumi, tetapi membentuk sudut 3^o23’. Kemiringan bidang orbit ini cukup kecil.

Jadi, sekarang Anda sudah tahu bagaimana salah satu metode menghitung jarak Bumi-Matahari yang dijadikan unit (satuan) jarak benda-benda lain di tata surya kita ini.

Salah satu metode lain untuk menghitung AU dengan ketelitian yang lebih rendah adalah menggunakan peristiwa transit Venus. Ketelitian yang lebih rendah disebabkan sulitnya menentukan secara pasti waktu kontak I (saat piringan Venus menyentuh piringan Matahari) dan kontak IV (saat piringan Venus meninggalkan piringan Matahari). Efek ini dikenal dengan blackdrop effect. Transit Venus adalah peristiwa ketika piringan Venus lewat di "depan" piringan Matahari (nampak seperti noda hitam di permukaan Matahari).

Peristiwa ini terakhir terjadi pada tanggal 8 Juni 2004 dan akan terjadi lagi pada tanggal 6 Juni 2012. Transit berikutnya lagi akan terjadi ratusan tahun lagi (pada 11 Desember 2117).

Data hasil pengamatan transit Venus tahun 1761 dan 1769 (oleh Edmund Halley):

The Observed Tracks of Venus across the Face of the Sun during the Transits of 1761 and 1769

Peristiwa transit ini dapat digunakan untuk menghitung paralaks Matahari.

Metode perhitungannya diajukan oleh Halley pada tahun 1776:

Dari gambar di atas dapat ditemukan hubungan:
D = d . Lv/(LE - Lv ) (dari hubungan kesebangunan segitiga)

Ratio Lv/LE dapat diketahui dari Hukum Ketiga Kepler. Secara kasar, nilai sama dengan sin θ (dimana θ adalah sudut elongansi terbesar planet Venus - lihat gambar di bawah ini)

Jadi, D = d . sin θ. L_E/(L_E( 1 - sin θ)) = d . sin θ/( 1 - sin θ)

Oleh sebab itu, dari ratio D/H (lihat gambar sebelumnya), nilai H (diameter Matahari) dapat dhitung. Kemudian, nilai paralaks Matahari dan jarak Matahari dari Bumi (1 AU) dapat dihitung. Memang metode ini, nampak lebih sulit dibandingkan metode dengan radar tetapi pada saat itu belum ada cara langsung untuk mengukur jarak Bumi ke Venus.

Sekarang Anda diminta untuk mencoba menghitung jarak Bumi-Matahari berdasarkan metode Halley. Diketahui paralaks Matahari hasil perhitungan Halley antara 8.55" sampai 8.88". Jawabannya boleh disampaikan lewat kolom komentar.

Sumber :

1. Slide kuliah Astrofisika 1 : Bab Besaran Mendasar dalam Astrofisika, oleh Dr. Djoni N. Dawanas, ITB.
2. wikipedia.org
3. The transit of Venus and The Quest For the Solar Parallax, by David Sellers (Leeds, England)
4. NASA

Di bawah ini juga disediakan 2 file artikel tentang perhitungan AU yang dapat Anda download dari link di bawah ini:

1. Venus Transit
2. Quest for the Astronomical Unit
3. Transit of Venus 2004, Calculation of the Astronomical Unit from the transit durations at two different locations

Selamat belajar.

Kompetisi Karya Tulis Astronomi

Buat rekan-rekan muda pecinta astronomi, ada sebuah berita gembira untuk anda. The International Year of Astronomy 2009 bersama International Astronomical Union dan UNESCO bekerja sama membawa penduduk bumi untuk menemukan kembali tempatnya di alam semesta melalui keindahan langit malam maupun cerahnya angkasa di siang hari. Selain itu diharapkan berlangsungnya tahun astronomi 2009 diharapkan dapat menumbuhkan ketertarikan pribadi akan kemegahan alam semesta maupun sebuah penemuan baru.

Kali ini Space Generation Advisory Council (SGAC) mengadakan sebuah kompetisi essay dengan tema :

“What Astronomy means to you?”

Kompetisi ini didedikasikan pada astronom muda untuk mengekspresikan perasaan dan pikirannya secara kreatif. 2 Pemenang pertama akan diundang ke Paris untuk berpartisipasi dalam acara “Launch Conference of the International Year of Astronomy” pada tanggal 14-18 Jan 2009. Panitia akan menanggung biaya selama di Paris, namun biaya perjalanan menjadi tanggung jawab penulis (pemenang).Biaya perjalanan dan akomodasi akan menjadi tanggungan panitia.

Syarat keikutsertaan :

1. Penulis harus berusia 18-22 tahun.
2. Essay maksimum memuat 2500 kata, dengan abstrak maksimum 200 kata harus disertakan saat pendaftaran.
3. Essays ditulis dalam bahasa Inggris. Tidak diperlukan pengejaan tingkat tinggi untuk para penulis yang bahasa ibunya bukan bahasa Inggris.
4. Essay ditulis dengan huruf (font) Times New Roman 11, spasi dobel dan dikirim dalam format .doc atau .pdf
5. Essay saat diserahkan sudah dalam keadaaan siap dipublikasikan tanpa catatan kaki.

Panitia penilaian akan menilai berdasarkan kriteria berikut:

• Inspirasi akan astronomi
• inovasi dan originalitas
• keterkaitan dengan IYA2009
• Kualitas dalam gaya penulisan dan struktur penulisan.

Tenggat Waktu:
Tulisan / essay sudah harus dikirimkan melalui email ke :
bee@spacegeneration.org
28 November 2008, 17:00 GMT atau 23.00 wib

Keterangan lebih lengkap bisa dibaca di :
http://www.spacegeneration.org/node/2202

Sumber: Langit Selatan - Situs Astronomi Indonesia

Deepest Ultraviolet Image Shows a Sea of Distant Galaxies

Caption : A Pool of Distant Galaxies. Credit: ESO

Dive right in to this image that contains a sea of distant galaxies! The Very Large Telescope has obtained the deepest ground-based image in the ultraviolet band, and here, you can see this patch of the sky is almost completely covered by galaxies, each one, like our own Milky Way galaxy, and home of hundreds of billions of stars. A few notable things about this image: galaxies were detected that are a billion times fainter than the unaided eye can see, and also in colors not directly observable by the human eye. In this image, a large number of new galaxies were discovered that are so far away that they are seen as they were when the Universe was only 2 billion years old! Also…

This image contains more than 27 million pixels and is the result of 55 hours of observation, made primarily with the Visible Multi Object Spectrograph (VIMOS) instrument. To get the full glory of this image, here's where you can download the full resolution version. It's worth the wait while it downloads. Or click here to be able to zoom around the image.

In this sea of galaxies – or island universes as they are sometimes called – only a very few stars belonging to the Milky Way are seen. One of them is so close that it moves very fast on the sky. This "high proper motion star" is visible to the left of the second brightest star in the image. It appears as a funny elongated rainbow because the star moved while the data were being taken in the different filters over several years.

The VLT folks describe this image as a "uniquely beautiful patchwork image, with its myriad of brightly coloured galaxies." It shows the Chandra Deep Field South (CDF-S), one of the most observed and best studied regions in the entire sky. The CDF-S is one of the two regions selected as part of the Great Observatories Origins Deep Survey (GOODS), an effort of the worldwide astronomical community that unites the deepest observations from ground- and space-based facilities at all wavelengths from X-ray to radio. Its primary purpose is to provide astronomers with the most sensitive census of the distant Universe to assist in their study of the formation and evolution of galaxies.

The image encompasses 40 hours of observations with the VLT, just staring at the same region of the sky. The VIMOS R-band image was obtained co-adding a large number of archival images totaling 15 hours of exposure.

Source: ESO
Cited from : universetoday

Chandra Telescope Searches for Antimatter

The Bullet Cluster.

Credit: X-ray: NASA/CXC/CfA/M.Markevitch et al.;
Optical: NASA/STScI; Magellan/U.Arizona/D.Clowe et al.

Say the word "antimatter" and immediately people think of science fiction – anti-universes, fuel for the Enterprise's warp-speed engines and so forth. But Captain, we can't change the laws of physics; antimatter is the real deal. Antimatter is made up of elementary particles, each of which has the same mass as their corresponding matter counterparts –protons, neutrons and electrons — but the opposite charges and magnetic properties. When matter and antimatter particles collide, they annihilate each other and produce energy according to Einstein's famous equation, E=mc2. But antimatter isn't something that's available on every corner drugstore (and neither is plutonium, to continue with the movie theme) and there's not very much of it around, so it seems. But, according to theory, it wasn't always that way, and scientists are using the Chandra X-ray Observatory to hunt for evidence of antimatter that was present in the very early universe. And it's not an easy job…

According to the Big Bang model, the Universe was awash in particles of both matter and antimatter shortly after the Big Bang. Most of this material annihilated, but because there was slightly more matter than antimatter - less than one part per billion - only matter was left behind, at least in the local Universe.

Trace amounts of antimatter are believed to be produced by powerful phenomena such as relativistic jets powered by black holes and pulsars, but no evidence has yet been found for antimatter remaining from the infant Universe.

How could any primordial antimatter have survived? Just after the Big Bang there was believed to be an extraordinary period, called inflation, when the Universe expanded exponentially in just a fraction of a second.

"If clumps of matter and antimatter existed next to each other before inflation, they may now be separated by more than the scale of the observable Universe, so we would never see them meet," said Gary Steigman of The Ohio State University, who conducted

the study. "But, they might be separated on smaller scales, such as those of superclusters or clusters, which is a much more interesting possibility."

Illustration of Antimatter/Matter Annihilation. (NASA/CXC/M. Weiss)

In that case, collisions between two galaxy clusters, the largest gravitationally-bound structures in the Universe, might show evidence for antimatter. X-ray emission shows how much hot gas is involved in such a collision. If some of the gas from either cluster has particles of antimatter, then there will be annihilation and the X-rays will be accompanied by gamma rays. Steigman used data obtained by Chandra and now de-orbited Compton Gamma Ray Observatory to study the Bullet Cluster, where two large clusters of galaxies have crashed into one another at extremely high velocities. At a relatively close distance and with a favorable side-on orientation as viewed from Earth, the Bullet Cluster provides an excellent test site to search for the signal for antimatter.

"This is the largest scale over which this test for antimatter has ever been done," said Steigman, whose paper was published in the Journal of Cosmology and Astroparticle Physics. "I'm looking to see if there could be any clusters of galaxies which are made of large amounts of antimatter." The observed amount of X-rays from Chandra and the non-detection of gamma rays from the Compton data show that the antimatter fraction in the Bullet Cluster is less than three parts per million. Moreover, simulations of the Bullet Cluster merger show that these results rule out any significant amounts of antimatter over scales of about 65 million light years, an estimate of the original separation of the two colliding clusters. "The collision of matter and antimatter is the most efficient process for generating energy in the Universe, but it just may not happen on very large scales," said Steigman. "But, I'm not giving up yet as I'm planning to look at other colliding galaxy clusters that have recently been discovered." Finding antimatter in the Universe might tell scientists about how long the period of inflation lasted. "Success in this experiment, although a long shot, would teach us a lot about the earliest stages of the Universe," said Steigman. Tighter constraints have been placed by Steigman on the presence of antimatter on smaller scales by looking at single galaxy clusters that do not involve such large, recent collisions.

Source: Chandra/Harvard and written by Nancy Atkinson

Cited from : universetoday.com

Trivia : Mengenali Konstelasi (Rasi) Bintang

Coba Anda sebutkan 2 rasi bintang yang terlihat pada gambar di atas.

Di arah langit manakah (utara, selatan, timur atau barat) foto langit tersebut di ambil?
Jawaban silakan Anda disampaikan lewat kolom komentar.
Selamat mencoba.

Animasi Gerak Bumi-Bulan

Titik hijau menunjukkan suatu lokasi tertentu di permukaan Bumi. Perhatikan bahwa permukaan Bulan yang menghadap Bumi selalu kurang lebih sama tetapi Bulan.
Penyebabnya adalah periode rotasi bulan sama dengan periode revolusi Bulan, yaitu sekitar 27 1/3 hari.
Semoga dengan mengamati animasi ini, Anda bisa lebih memahami mekanisme gerak Bumi dan Bulan.

Trivia Questions : Can You Mention These Objects' Name?

Apakah Anda bisa menyebutkan nama-nama ke sepuluh objek yang ditampilkan dalam gambar di bawah ini?

Gambar objek 1


Gambar objek 2 hingga 10

Anda dipersilakan mencoba menyampaikan jawaban lewat kolom komentar.

Pengenalan Fotometri (Bagian 2)

Sistem Magnitudo

Materi yang berikutnya akan dibahas sebagai rangkaian pengenalan akan fotometri adalah sistem magnitudo. Magnitudo adalah suatu sistem skala ukuran kecerlangan bintang. Sistem magnitudo ini dibuat pertama kali oleh Hipparchus pada abad 2 sebelum masehi. Dia membagi terang bintang menjadi 6 kelompok berdasarkan penampakkannya dengan mata telanjang. Bintang yang paling terang diberi magnitudo 1 sedangkan bintang yang paling lemah yang bisa diamati oleh mata telanjang diberi magnitudo 6. Hal yang perlu diperhatikan bahwa semakin terang suatu bintang, semakin kecil magnitudonya. Kelemahan sistem ini adalah tidak adanya suatu standar baku tentang terang bintang dan penentuan skala ini sangat tergantung pada kejelian dan kualitas mata pengamat (karena bersifat kualitatif)

Ilmuwan John Herschel mendapatkan bahwa kepekaan mata dalam menilai terang bintang bersifat logaritmik. Bintang yang bermagnitudo 1 ternyata 100 kali lebih terang dibandingkan bintang yang bermagnitudo 6. Berdasarkan fakta ini, Pogson merumuskan skala magnitudo secara kuantitatif. Hal ini menyebabkan sistem magnitudo semakin banyak digunakan hingga saat ini.

Skala Pogson untuk magnitudo (semu):

m₁ - m₂ = -2,5log(E₁/E₂)

dengan :
m₁ : magnitudo (semu) bintang 1
m₂ : magnitudo (semu) bintang 2
E₁ : Fluks pancaran yang diterima pengamat dari bintang 1
E₂ : Fluks pancaran yang diterima pengamat dari bintang 2

Harga acuan (pembanding standar) skala magnitudo mula-mula digunakan bintang Polaris. Bintang Polaris ditetapkan memiliki magnitudo 2 dan bintang lainnya dibandingkan terhadap bintang Polaris. Bintang Polaris, yang juga bintang kutub langit utara, dipilih karena bintang ini terlihat dari seluruh observatorium yang ada di belahan bumi utara (karena pada masa itu, belahan bumi utara lebih berkembang dan maju secara teknologi). Namun, bintang ini ternyata memiliki kecerlangan yang berubah-ubah (Polaris ternyata adalah sebuah bintang variabel Cepheid) sehingga kecerlangan Polaris tidak bisa digunakan sebagai patokan/standar baku. Oleh sebab itu, astronom menentukan bintang - bintang lainnya untuk dijadikan standar.

Untuk mengukur kecerlangan suatu bintang digunakan alat yang dinamakan fotometer. Prinsip kerjanya adalah dengan memanfaatkan gejala fotolistrik. Efek fotolistrik inilah yang membuat Einstein memperoleh hadiah Nobel (dan bukan karena hukum relativitas). Penerapan efek fotolistrik ini antara lain diterapkan pada sel surya, chip CCD, dll. Cahaya (atau gelombang elektromagnetik lainnya) ketika menyentuh kelompok bahan tertentu akan menyebabkan elektron yang ada di permukaan bahan akan terlepas. Jumlah elektron yang terlepas tergantung dari intensitas radiasi gelombang elektromagnetik yang diterimanya. Jumlah elektron yang dihasilkan ini dapat menghasikan arus listrik yang dapat kita ukur. Dengan prinsip inilah, kita dapat mengukur intensitas cahaya sebuah bintang.

Cara terbaik untuk mengukur magnitudo adalah dengan membandingkan kecerlangan suatu bintang dengan bintang standar yang ada di dekatnya. Hal ini disebabkan perbedaan keadaan atmosfer antara kedua bintang (bintang standar dan bintang program/yang diamati) tidaklah besar. Atmosfer Bumi dapat menyerap sebagian cahaya bintang dan besarnya penyerapan tergantung dari ketinggian dan kondisi atmosfer yang dilewati cahaya bintang sebelum sampai ke detektor pengamat. Pada saat ini, sudah banyak bintang standar, baik di langit belahan utara maupun selatan.

Magnitudo yang kita bahas di atas merupakan ukuran terang bintang yang kita lihat atau terang semu (ada faktor jarak dan penyerapan yang harus diperhitungkan). Magnitudo yang menyatakan ukuran fluks energi bintang yang kita terima/ukuran terang bintang yang kita lihat/jumlah foton yang kita terima disebut magnitudo semu (apparent magnitude).

Untuk menyatakan luminositas atau kuat sebenarnya sebuah bintang, kita definisikan besaran magnitudo mutlak (intrinsic/absolute magnitude), yaitu magnitudo bintang yang diandaikan diamati dari jarak 10 pc.

Skala Pogson untuk magnitudo mutlak (M) :

M₁ - M₂ = -2,5log(L₁/L₂)

dengan :
M₁ : magnitudo mutlak bintang 1
M₂ : magnitudo mutlak bintang 2
L₁ : Luminositas bintang 1
L₂ : Luminositas bintang 2

Hubungan antara magnitudo semu (m) dan magnitudo mutlak (M) disebut modulus jarak.

m - M = -5 + 5 log d

dengan d adalah jarak bintang (dalam pc) dan (m-M) disebut modulus jarak.

Persamaan modulus jarak umumnya digunakan dalam menentukan jarak bintang-bintang yang jauh secara tidak langsung (metode indirect). Seperti yang sudah pernah dibahas sebelumnya bahwa metode paralaks trigonometri hanya bisa menentukan jarak secara akurat untuk beberapa bintang dengan jarak kurang dari 500 pc. Untuk bintang yang lebih jauh lagi, perlu digunakan metode-metode tak langsung (indirect). Salah satunya adalah dengan mengukur magnitudo semu bintang lalu memperkirakan magnitudo mutlaknya. Cara memperkirakan magnitudo mutlak ini banyak metode/caranya. Dengan mengetahui magnitudo semu dan perkiraan magnitudo mutlak, maka kita bisa memperkirakan jarak suatu bintang dengan modulus jarak.

Hal yang perlu diperhatikan adalah persamaan modulus jarak di atas valid/benar/akurat jika diasumsikan tidak ada materi antar bintang yang terletak di antara arah pandang kita ke bintang. Materi antar bintang tersebut dapat mengabsorpsi sebagian cahaya bintang. Jika keberadaan serapan oleh materi antar bintang (MAB) tidak diabaikan, maka persamaan modulus jaraknya :

m - M = -5 + 5 log d + A_V

dengan A_V : konstanta serapan materi antar bintang.

Contoh:
Magnitudo mutlak sebuah bintang adalah M = 5 dan magnitudo semunya adalah m = 10. Jika absorpsi oleh materi antar bintang diabaikan, berapakah jarak bintang tersebut ?

Jawab : m = 10 dan M = 5, dari rumus Pogson
m – M = -5 + 5 log d
diperoleh, 10 – 5 = -5 + 5 log d
5 log d = 10
log d = 2 --> d = 100 pc

Sebelum perkembangan fotografi, magnitudo bintang ditentukan dengan mata. Kepekaan mata untuk daerah panjang gelombang yang berbeda tidak sama. Mata terutama peka untuk cahaya kuning hijau di daerah λ = 5 500 Å, karena itu magnitudo yang diukur pada daerah ini disebut magnitudo visual atau m_vis.

Dengan berkembangnya fotografi, magnitudo bintang selanjutnya ditentukan secara fotografi. Pada awal fotografi, emulsi fotografi mempunyai kepekaan di daerah biru-ungu pada panjang gelombang sekitar 4.500 Å. Magnitudo yang diukur pada daerah ini disebut magnitudo fotografi atau m_fot .

Jadi, untuk suatu bintang, m_vis berbeda dari m_fot. Selisih kedua magnitudo tersebut, yaitu magnitudo fotografi dikurang magnitudo visual disebut indeks warna (Color Index – CI).
Semakin panas atau makin biru suatu bintang, semakin kecil indeks warnanya.

Dengan berkembangnya fotografi, selanjutnya dapat dibuat pelat foto yang peka terhadap daerah panjang gelombang lainnya, seperti kuning, merah bahkan inframerah.

Pada tahun 1951, H.L. Johnson dan W.W. Morgan mengajukan sistem magnitudo yang disebut sistem UBV, yaitu :

U = magnitudo semu dalam daerah ultraungu (λ_ef = 3500 Å)
B = magnitudo semu dalam daerah biru ( λef = 4350 Å)
V = magnitudo semu dalam daerah visual ( λef = 5550 Å)

Dalam sistem UBV ini, indeks warna adalah U-B dan B-V. Semakin panas suatu bintang, semakin kecil nilai (B-V) nya.

Dewasa ini pengamatan fotometri tidak lagi menggunakan pelat film, tetapi dilakukan dengan kamera CCD, sehingga untuk menentukan bermacam-macam sistem magnitudo tergantung pada filter yang digunakan.

Contoh:
Tiga bintang diamati magnitudo dalam panjang gelombang visual (V) dan biru (B) seperti yang diperlihatkan dalam tabel di bawah.

No.	B	V
1	8,52	8,82
2	7,45	7,25
3	7,45	6,35

1. Tentukan bintang nomor berapakah yang paling terang ? Jelaskanlah alasannya
2. Bintang yang anda pilih sebagai bintang yang paling terang itu dalam kenyataannya apakah benar-benar merupakan bintang yang paling terang ? Jelaskanlah jawaban anda.
3. Tentukanlah bintang mana yang paling panas dan mana yang paling dingin. Jelaskanlah alasannya.

Jawab:

1. Bintang paling terang adalah bintang yang magnitudo visualnya paling kecil. Dari tabel tampak bahwa bintang yang magnitudo visualnya paling kecil adalah bintang no. 3, jadi bintang yang paling terang adalah bintang no. 3
2. Belum tentu karena terang suatu bintang bergantung pada jaraknya ke pengamat seperti terlihat pada rumus yang sudah dijelaskan sebelumnya. Oleh karena itu bintang yang sangat terang bisa tampak sangat lemah cahayanya karena jaraknya yang jauh.
3. Untuk menjawab pertanyaan-pertanyaan ini kita tentukan dahulu indeks warna ketiga bintang tersebut, karena makin panas atau makin biru sebuah bintang maka semakin kecil indeks warnanya.

Nomor bintang	B	V	B - V
1.	8,52	8,82	-0,30
2.	7,45	7,25	0,20
3.	7,45	6,35	1,10

Dari tabel di atas tampak bahwa bintang yang mempunyai indeks warna terkecil adalah bintang no. 1. Jadi bintang terpanas adalah bintang no. 1.

Magnitudo Bolometrik
Sistem magnitudo yang sudah kita bahas di atas hanya diukur pada panjang gelombang tertentu saja (m_vis,m_fot,m_B,m_U). Walaupun berbagai magnitudo tersebut dapat menggambarkan sebaran energi pada spektrum bintang sehingga dapat memberikan petunjuk mengenai temperaturnya, namun belum dapat memberikan informasi mengenai sebaran energi pada seluruh panjang gelombang yang dipancarkan oleh suatu bintang. Oleh sebab itu, didefinisikanlah sistem magnitudo bolometrik (m_bol) yang menyatakan magnitudo bintang yang diukur dalam seluruh panjang gelombang.

Magnitudo mutlak bolometrik bintang sangat penting karena dapat digunakan untuk mengetahui luminositas dari sebuah bintang (energi total yang dipancarkan permukaan bintang per detik) dengan membandingkannya dengan magnitudo mutlak bolometrik Matahari.
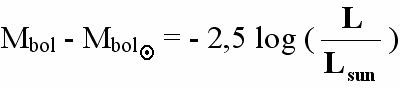
Dengan M_bol = magnitudo mutlak bolometrik bintang
M_bol¤ = magnitudo mutlak bolometrik Matahari (4,74)

Persamaan modulus jarak untuk magnitudo bolometrik (absorpsi MAB diabaikan):

m_bol - M_bol = -5 + 5log d

dengan d dalam parsec.

Apabila M_bol suatu bintang dapat ditentukan, maka luminositasnya juga dapat ditentukan (dapat dinyatakan dalan luminositas Matahari). Luminositas bintang merupakan parameter yang sangat penting dalam teori evolusi bintang. Sayangnya, magnitudo mutlak bolometrik sangat sukar ditentukan, karena beberapa panjang gelombang tidak dapat menembus atmosfer bumi. Untuk bintang yang panas, sebagian energinya dipancarkan pada daerah ultraviolet. Untuk bintang yang dingin, sebagian energinya dipancarkan pada daerah inframerah. Oleh karena itu, pengamatan magnitudo bolometrik harus dilakukan di atas atmosfer.

Untuk memudahkan, magnitudo bolometrik ditentukan secara teori berdasarkan pengamatan di bumi. Atau, dapat ditentukan secara tidak langsung, yaitu dengan memberikan koreksi pada magnitudo visualnya, yang disebut koreksi bolometrik (Bolometric Correction - BC).

m_v – m_bol = BC

M_v – M_bol = BC

Nilai BC tergantung pada temperatur atau warna bintang.

Untuk bintang yang sangat panas, sebagian besar energinya dipancarkan pada daerah ultraviolet sedangkan untuk bintang yang sangat dingin, sebagian besar energinya dipancarkan pada daerah inframerah (hanya sebagian kecil saja pada daerah visual). Untuk bintang-bintang seperti ini, harga BC-nya besar. Untuk bintang-bintang yang bertemperatur sedang, sebagian besar energinya dipancarkan pada daerah visual, sehingga harga BC-nya kecil.

Karena harga BC bergantung pada warna bintang, maka kita dapat mencari hubungan antara BC dan indeks warna (B-V). Untuk bintang yang dapat ditentukan magnitudo bolometriknya. Didefinisikan bahwa harga terkecil BC adalah nol (BC ≥ 0). Untuk BC = 0 untuk (B-V) = 0,3.

Hubungan antara nilai BC dengan indeks warna (CI) ditunjukkan dalam grafik di bawah ini:
Untuk Matahari, magnitudo bolometriknya (m_bol¤) = -26,83, magnitudo mutlak bolometriknya adalah M_bol¤ = 4,74 dan koreksi bolometriknya BC = 0,08. Berikut disajikan tabel temperatur efektif dan koreksi bolometrik untuk bintang-bintang deret utama dan bintang maharaksasa.

B - V	Bintang deret utama		Bintang maharaksasa
	Tef	BC	Tef	BC
- 0,25	24500	2,30	26000	2,20
- 0,23	21000	2,15	23500	2,05
- 0,20	17700	1,80	19100	1,72
- 0,15	14000	1,20	14500	1,12
- 0,10	11800	0,61	12700	0,53
- 0,01	10500	0,33	11000	0,14
0,00	9480	0,15	9800	- 0,01
0,10	8530	0,04	8500	- 0,09
0,20	7910	0	7440	- 0,10
0,30	7450	0	6800	- 0,10
0,40	6800	0	6370	- 0,09
0,50	6310	0,03	6020	- 0,07
0,60	5910	0,07	5800	- 0,003
0,70	5540	0,12	546	0,003
0,80	5330	0,19	5200	0,10
0,90	5090	0,28	4980	0,19
1,00	4840	0,40	4770	0,30
1,20	4350	0,75	4400	0,59

Latihan:

1. Bintang A tampak mempunyai kecerlangan yang sama pada filter merah dan biru. Bintang B tampak lebih terang pada filter merah daripada filter biru. Bintang C tampak lebih terang pada filter biru daripada di filter merah. Urutkan bintang-bintang itu berdasarkan pertambahan temperaturnya.
2. The binary star Capella has a total magnitude of 0.21^m and the two components differ in magnitude by 0.5^m. The parallax of Capella is 0.063”. Calculate the absolute magnitudes of the two components.
3. There are about 250 millions of the stars in the elliptical galaxy M32. The visual magnitude of this galaxy is 9. If the luminosities of all are equal, what is the visual magnitude of one star in this galaxy?
4. Two stars have the same apparent magnitude and are of the same spectral type. One is twice as far away as the other. What is the relative size of the two stars?
   
5. Sebuah galaksi diamati memiliki magnitudo visual m_V = 21. Magnitudo ini berasosiasi dengan energi dari 10¹¹ bintang yang ada di dalamnya (terdiri dari 3 jenis). Perkirakan/hitung jarak galaksi tersebut. Untuk itu gunakan asumsi sebagai berikut
   

Jenis bintang	MV	Jumlah (%)
a	1	20
b	4	50
c	6	30

Sumber : Djoni D. Dawanas

Jika ada kesulitan atau pertanyaan tentang materi ini, silakan coba disampaikan lewat kolom komentar. Selamat belajar.