Trivia : Mengenali Konstelasi (Rasi) Bintang

Coba Anda sebutkan 2 rasi bintang yang terlihat pada gambar di atas.

Di arah langit manakah (utara, selatan, timur atau barat) foto langit tersebut di ambil?
Jawaban silakan Anda disampaikan lewat kolom komentar.
Selamat mencoba.

Animasi Gerak Bumi-Bulan

Titik hijau menunjukkan suatu lokasi tertentu di permukaan Bumi. Perhatikan bahwa permukaan Bulan yang menghadap Bumi selalu kurang lebih sama tetapi Bulan.
Penyebabnya adalah periode rotasi bulan sama dengan periode revolusi Bulan, yaitu sekitar 27 1/3 hari.
Semoga dengan mengamati animasi ini, Anda bisa lebih memahami mekanisme gerak Bumi dan Bulan.

Trivia Questions : Can You Mention These Objects' Name?

Apakah Anda bisa menyebutkan nama-nama ke sepuluh objek yang ditampilkan dalam gambar di bawah ini?

Gambar objek 1


Gambar objek 2 hingga 10

Anda dipersilakan mencoba menyampaikan jawaban lewat kolom komentar.

Pengenalan Fotometri (Bagian 2)

Sistem Magnitudo

Materi yang berikutnya akan dibahas sebagai rangkaian pengenalan akan fotometri adalah sistem magnitudo. Magnitudo adalah suatu sistem skala ukuran kecerlangan bintang. Sistem magnitudo ini dibuat pertama kali oleh Hipparchus pada abad 2 sebelum masehi. Dia membagi terang bintang menjadi 6 kelompok berdasarkan penampakkannya dengan mata telanjang. Bintang yang paling terang diberi magnitudo 1 sedangkan bintang yang paling lemah yang bisa diamati oleh mata telanjang diberi magnitudo 6. Hal yang perlu diperhatikan bahwa semakin terang suatu bintang, semakin kecil magnitudonya. Kelemahan sistem ini adalah tidak adanya suatu standar baku tentang terang bintang dan penentuan skala ini sangat tergantung pada kejelian dan kualitas mata pengamat (karena bersifat kualitatif)

Ilmuwan John Herschel mendapatkan bahwa kepekaan mata dalam menilai terang bintang bersifat logaritmik. Bintang yang bermagnitudo 1 ternyata 100 kali lebih terang dibandingkan bintang yang bermagnitudo 6. Berdasarkan fakta ini, Pogson merumuskan skala magnitudo secara kuantitatif. Hal ini menyebabkan sistem magnitudo semakin banyak digunakan hingga saat ini.

Skala Pogson untuk magnitudo (semu):

m₁ - m₂ = -2,5log(E₁/E₂)

dengan :
m₁ : magnitudo (semu) bintang 1
m₂ : magnitudo (semu) bintang 2
E₁ : Fluks pancaran yang diterima pengamat dari bintang 1
E₂ : Fluks pancaran yang diterima pengamat dari bintang 2

Harga acuan (pembanding standar) skala magnitudo mula-mula digunakan bintang Polaris. Bintang Polaris ditetapkan memiliki magnitudo 2 dan bintang lainnya dibandingkan terhadap bintang Polaris. Bintang Polaris, yang juga bintang kutub langit utara, dipilih karena bintang ini terlihat dari seluruh observatorium yang ada di belahan bumi utara (karena pada masa itu, belahan bumi utara lebih berkembang dan maju secara teknologi). Namun, bintang ini ternyata memiliki kecerlangan yang berubah-ubah (Polaris ternyata adalah sebuah bintang variabel Cepheid) sehingga kecerlangan Polaris tidak bisa digunakan sebagai patokan/standar baku. Oleh sebab itu, astronom menentukan bintang - bintang lainnya untuk dijadikan standar.

Untuk mengukur kecerlangan suatu bintang digunakan alat yang dinamakan fotometer. Prinsip kerjanya adalah dengan memanfaatkan gejala fotolistrik. Efek fotolistrik inilah yang membuat Einstein memperoleh hadiah Nobel (dan bukan karena hukum relativitas). Penerapan efek fotolistrik ini antara lain diterapkan pada sel surya, chip CCD, dll. Cahaya (atau gelombang elektromagnetik lainnya) ketika menyentuh kelompok bahan tertentu akan menyebabkan elektron yang ada di permukaan bahan akan terlepas. Jumlah elektron yang terlepas tergantung dari intensitas radiasi gelombang elektromagnetik yang diterimanya. Jumlah elektron yang dihasilkan ini dapat menghasikan arus listrik yang dapat kita ukur. Dengan prinsip inilah, kita dapat mengukur intensitas cahaya sebuah bintang.

Cara terbaik untuk mengukur magnitudo adalah dengan membandingkan kecerlangan suatu bintang dengan bintang standar yang ada di dekatnya. Hal ini disebabkan perbedaan keadaan atmosfer antara kedua bintang (bintang standar dan bintang program/yang diamati) tidaklah besar. Atmosfer Bumi dapat menyerap sebagian cahaya bintang dan besarnya penyerapan tergantung dari ketinggian dan kondisi atmosfer yang dilewati cahaya bintang sebelum sampai ke detektor pengamat. Pada saat ini, sudah banyak bintang standar, baik di langit belahan utara maupun selatan.

Magnitudo yang kita bahas di atas merupakan ukuran terang bintang yang kita lihat atau terang semu (ada faktor jarak dan penyerapan yang harus diperhitungkan). Magnitudo yang menyatakan ukuran fluks energi bintang yang kita terima/ukuran terang bintang yang kita lihat/jumlah foton yang kita terima disebut magnitudo semu (apparent magnitude).

Untuk menyatakan luminositas atau kuat sebenarnya sebuah bintang, kita definisikan besaran magnitudo mutlak (intrinsic/absolute magnitude), yaitu magnitudo bintang yang diandaikan diamati dari jarak 10 pc.

Skala Pogson untuk magnitudo mutlak (M) :

M₁ - M₂ = -2,5log(L₁/L₂)

dengan :
M₁ : magnitudo mutlak bintang 1
M₂ : magnitudo mutlak bintang 2
L₁ : Luminositas bintang 1
L₂ : Luminositas bintang 2

Hubungan antara magnitudo semu (m) dan magnitudo mutlak (M) disebut modulus jarak.

m - M = -5 + 5 log d

dengan d adalah jarak bintang (dalam pc) dan (m-M) disebut modulus jarak.

Persamaan modulus jarak umumnya digunakan dalam menentukan jarak bintang-bintang yang jauh secara tidak langsung (metode indirect). Seperti yang sudah pernah dibahas sebelumnya bahwa metode paralaks trigonometri hanya bisa menentukan jarak secara akurat untuk beberapa bintang dengan jarak kurang dari 500 pc. Untuk bintang yang lebih jauh lagi, perlu digunakan metode-metode tak langsung (indirect). Salah satunya adalah dengan mengukur magnitudo semu bintang lalu memperkirakan magnitudo mutlaknya. Cara memperkirakan magnitudo mutlak ini banyak metode/caranya. Dengan mengetahui magnitudo semu dan perkiraan magnitudo mutlak, maka kita bisa memperkirakan jarak suatu bintang dengan modulus jarak.

Hal yang perlu diperhatikan adalah persamaan modulus jarak di atas valid/benar/akurat jika diasumsikan tidak ada materi antar bintang yang terletak di antara arah pandang kita ke bintang. Materi antar bintang tersebut dapat mengabsorpsi sebagian cahaya bintang. Jika keberadaan serapan oleh materi antar bintang (MAB) tidak diabaikan, maka persamaan modulus jaraknya :

m - M = -5 + 5 log d + A_V

dengan A_V : konstanta serapan materi antar bintang.

Contoh:
Magnitudo mutlak sebuah bintang adalah M = 5 dan magnitudo semunya adalah m = 10. Jika absorpsi oleh materi antar bintang diabaikan, berapakah jarak bintang tersebut ?

Jawab : m = 10 dan M = 5, dari rumus Pogson
m – M = -5 + 5 log d
diperoleh, 10 – 5 = -5 + 5 log d
5 log d = 10
log d = 2 --> d = 100 pc

Sebelum perkembangan fotografi, magnitudo bintang ditentukan dengan mata. Kepekaan mata untuk daerah panjang gelombang yang berbeda tidak sama. Mata terutama peka untuk cahaya kuning hijau di daerah λ = 5 500 Å, karena itu magnitudo yang diukur pada daerah ini disebut magnitudo visual atau m_vis.

Dengan berkembangnya fotografi, magnitudo bintang selanjutnya ditentukan secara fotografi. Pada awal fotografi, emulsi fotografi mempunyai kepekaan di daerah biru-ungu pada panjang gelombang sekitar 4.500 Å. Magnitudo yang diukur pada daerah ini disebut magnitudo fotografi atau m_fot .

Jadi, untuk suatu bintang, m_vis berbeda dari m_fot. Selisih kedua magnitudo tersebut, yaitu magnitudo fotografi dikurang magnitudo visual disebut indeks warna (Color Index – CI).
Semakin panas atau makin biru suatu bintang, semakin kecil indeks warnanya.

Dengan berkembangnya fotografi, selanjutnya dapat dibuat pelat foto yang peka terhadap daerah panjang gelombang lainnya, seperti kuning, merah bahkan inframerah.

Pada tahun 1951, H.L. Johnson dan W.W. Morgan mengajukan sistem magnitudo yang disebut sistem UBV, yaitu :

U = magnitudo semu dalam daerah ultraungu (λ_ef = 3500 Å)
B = magnitudo semu dalam daerah biru ( λef = 4350 Å)
V = magnitudo semu dalam daerah visual ( λef = 5550 Å)

Dalam sistem UBV ini, indeks warna adalah U-B dan B-V. Semakin panas suatu bintang, semakin kecil nilai (B-V) nya.

Dewasa ini pengamatan fotometri tidak lagi menggunakan pelat film, tetapi dilakukan dengan kamera CCD, sehingga untuk menentukan bermacam-macam sistem magnitudo tergantung pada filter yang digunakan.

Contoh:
Tiga bintang diamati magnitudo dalam panjang gelombang visual (V) dan biru (B) seperti yang diperlihatkan dalam tabel di bawah.

No.	B	V
1	8,52	8,82
2	7,45	7,25
3	7,45	6,35

1. Tentukan bintang nomor berapakah yang paling terang ? Jelaskanlah alasannya
2. Bintang yang anda pilih sebagai bintang yang paling terang itu dalam kenyataannya apakah benar-benar merupakan bintang yang paling terang ? Jelaskanlah jawaban anda.
3. Tentukanlah bintang mana yang paling panas dan mana yang paling dingin. Jelaskanlah alasannya.

Jawab:

1. Bintang paling terang adalah bintang yang magnitudo visualnya paling kecil. Dari tabel tampak bahwa bintang yang magnitudo visualnya paling kecil adalah bintang no. 3, jadi bintang yang paling terang adalah bintang no. 3
2. Belum tentu karena terang suatu bintang bergantung pada jaraknya ke pengamat seperti terlihat pada rumus yang sudah dijelaskan sebelumnya. Oleh karena itu bintang yang sangat terang bisa tampak sangat lemah cahayanya karena jaraknya yang jauh.
3. Untuk menjawab pertanyaan-pertanyaan ini kita tentukan dahulu indeks warna ketiga bintang tersebut, karena makin panas atau makin biru sebuah bintang maka semakin kecil indeks warnanya.

Nomor bintang	B	V	B - V
1.	8,52	8,82	-0,30
2.	7,45	7,25	0,20
3.	7,45	6,35	1,10

Dari tabel di atas tampak bahwa bintang yang mempunyai indeks warna terkecil adalah bintang no. 1. Jadi bintang terpanas adalah bintang no. 1.

Magnitudo Bolometrik
Sistem magnitudo yang sudah kita bahas di atas hanya diukur pada panjang gelombang tertentu saja (m_vis,m_fot,m_B,m_U). Walaupun berbagai magnitudo tersebut dapat menggambarkan sebaran energi pada spektrum bintang sehingga dapat memberikan petunjuk mengenai temperaturnya, namun belum dapat memberikan informasi mengenai sebaran energi pada seluruh panjang gelombang yang dipancarkan oleh suatu bintang. Oleh sebab itu, didefinisikanlah sistem magnitudo bolometrik (m_bol) yang menyatakan magnitudo bintang yang diukur dalam seluruh panjang gelombang.

Magnitudo mutlak bolometrik bintang sangat penting karena dapat digunakan untuk mengetahui luminositas dari sebuah bintang (energi total yang dipancarkan permukaan bintang per detik) dengan membandingkannya dengan magnitudo mutlak bolometrik Matahari.
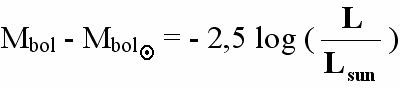Dengan M_bol = magnitudo mutlak bolometrik bintang
M_bol¤ = magnitudo mutlak bolometrik Matahari (4,74)

Persamaan modulus jarak untuk magnitudo bolometrik (absorpsi MAB diabaikan):

m_bol - M_bol = -5 + 5log d

dengan d dalam parsec.

Apabila M_bol suatu bintang dapat ditentukan, maka luminositasnya juga dapat ditentukan (dapat dinyatakan dalan luminositas Matahari). Luminositas bintang merupakan parameter yang sangat penting dalam teori evolusi bintang. Sayangnya, magnitudo mutlak bolometrik sangat sukar ditentukan, karena beberapa panjang gelombang tidak dapat menembus atmosfer bumi. Untuk bintang yang panas, sebagian energinya dipancarkan pada daerah ultraviolet. Untuk bintang yang dingin, sebagian energinya dipancarkan pada daerah inframerah. Oleh karena itu, pengamatan magnitudo bolometrik harus dilakukan di atas atmosfer.

Untuk memudahkan, magnitudo bolometrik ditentukan secara teori berdasarkan pengamatan di bumi. Atau, dapat ditentukan secara tidak langsung, yaitu dengan memberikan koreksi pada magnitudo visualnya, yang disebut koreksi bolometrik (Bolometric Correction - BC).

m_v – m_bol = BC

M_v – M_bol = BC

Nilai BC tergantung pada temperatur atau warna bintang.

Untuk bintang yang sangat panas, sebagian besar energinya dipancarkan pada daerah ultraviolet sedangkan untuk bintang yang sangat dingin, sebagian besar energinya dipancarkan pada daerah inframerah (hanya sebagian kecil saja pada daerah visual). Untuk bintang-bintang seperti ini, harga BC-nya besar. Untuk bintang-bintang yang bertemperatur sedang, sebagian besar energinya dipancarkan pada daerah visual, sehingga harga BC-nya kecil.

Karena harga BC bergantung pada warna bintang, maka kita dapat mencari hubungan antara BC dan indeks warna (B-V). Untuk bintang yang dapat ditentukan magnitudo bolometriknya. Didefinisikan bahwa harga terkecil BC adalah nol (BC ≥ 0). Untuk BC = 0 untuk (B-V) = 0,3.

Hubungan antara nilai BC dengan indeks warna (CI) ditunjukkan dalam grafik di bawah ini:
Untuk Matahari, magnitudo bolometriknya (m_bol¤) = -26,83, magnitudo mutlak bolometriknya adalah M_bol¤ = 4,74 dan koreksi bolometriknya BC = 0,08. Berikut disajikan tabel temperatur efektif dan koreksi bolometrik untuk bintang-bintang deret utama dan bintang maharaksasa.

B - V	Bintang deret utama		Bintang maharaksasa
	Tef	BC	Tef	BC
- 0,25	24500	2,30	26000	2,20
- 0,23	21000	2,15	23500	2,05
- 0,20	17700	1,80	19100	1,72
- 0,15	14000	1,20	14500	1,12
- 0,10	11800	0,61	12700	0,53
- 0,01	10500	0,33	11000	0,14
0,00	9480	0,15	9800	- 0,01
0,10	8530	0,04	8500	- 0,09
0,20	7910	0	7440	- 0,10
0,30	7450	0	6800	- 0,10
0,40	6800	0	6370	- 0,09
0,50	6310	0,03	6020	- 0,07
0,60	5910	0,07	5800	- 0,003
0,70	5540	0,12	546	0,003
0,80	5330	0,19	5200	0,10
0,90	5090	0,28	4980	0,19
1,00	4840	0,40	4770	0,30
1,20	4350	0,75	4400	0,59

Latihan:

1. Bintang A tampak mempunyai kecerlangan yang sama pada filter merah dan biru. Bintang B tampak lebih terang pada filter merah daripada filter biru. Bintang C tampak lebih terang pada filter biru daripada di filter merah. Urutkan bintang-bintang itu berdasarkan pertambahan temperaturnya.
2. The binary star Capella has a total magnitude of 0.21^m and the two components differ in magnitude by 0.5^m. The parallax of Capella is 0.063”. Calculate the absolute magnitudes of the two components.
3. There are about 250 millions of the stars in the elliptical galaxy M32. The visual magnitude of this galaxy is 9. If the luminosities of all are equal, what is the visual magnitude of one star in this galaxy?
4. Two stars have the same apparent magnitude and are of the same spectral type. One is twice as far away as the other. What is the relative size of the two stars?
   
5. Sebuah galaksi diamati memiliki magnitudo visual m_V = 21. Magnitudo ini berasosiasi dengan energi dari 10¹¹ bintang yang ada di dalamnya (terdiri dari 3 jenis). Perkirakan/hitung jarak galaksi tersebut. Untuk itu gunakan asumsi sebagai berikut
   

Jenis bintang	MV	Jumlah (%)
a	1	20
b	4	50
c	6	30

Sumber : Djoni D. Dawanas

Jika ada kesulitan atau pertanyaan tentang materi ini, silakan coba disampaikan lewat kolom komentar. Selamat belajar.

Pengenalan Fotometri (Bagian 1)

Fotometri adalah bagian dari astrofisika yang mempelajari kuantitas, kualitas dan arah pancaran radiasi elektromagnetik dari benda langit. Penggunaan kata ‘foto’ yang berarti ‘cahaya’ disebabkan pada awalnya pengamatan benda langit hanya terbatas pada panjang gelombang visual/optik.

Fotometri didasarkan pada pemahaman atas hukum pancaran (radiation law). Kita menghipotesakan bahwa benda langit diangggap memiliki sifat sebuah benda hitam (black body).

Sifat benda hitam antara lain :

1) pada kesetimbangan termal, temperatur benda hanya ditentukan oleh jumlah energi yang diserapnya per detik;

2) benda hitam tidak memancarkan radiasi pada seluruh gelombang elektromagnetik dengan intensitas yang sama (ada yang dominan meradiasikan gelombang elektromagnetik pada daerah biru dengan intensitas yang lebih besar dibandingkan gelombang elektromagnetik pada panjang gelombang lainnya. Konsekuensinya, benda tersebut akan nampak biru).

Panjang gelombang yang dipancarkan dengan intensitas maksimum (λ_maks) oleh sebuah benda hitam dengan temperatur T Kelvin adalah :

λ_maks = 0,2898/ T .......................... (pers. 1)

(λ_maks dinyatakan dalam cm dan T dalam Kelvin)

Persamaan di atas disebut dengan Hukum Wien.

Contoh penggunaan hukum Wien :
(Warning : Yang perlu diperhatikan bahwa λ_maks bukan berarti panjang gelombang maksimum tetapi panjang gelombang yang dipancarkan dengan intensitas maksimum)

Jumlah energi per satuan waktu yang dipancarkan sebuah benda hitam per satuan luas permukaan pemancar (benda hitam) disebut fluks energi yang dipancarkan. Besarnya fluks energi yang dipancarkan sebuah benda hitam (F) dengan temperatur T Kelvin adalah :

F = σT⁴ .......................... (pers. 2)

(σ : konstanta Stefan-Boltzman : 5,67 x 10^-8 Watt/m²K⁴)

Sedangkan total energi per waktu / daya yang dipancarkan sebuah benda hitam dengan luas permukaan pemancar A dan temperatur T Kelvin disebut dengan Luminositas. Besarnya luminositas (L) dihitung dengan persamaan :

L = A σT⁴ .......................... (pers. 3)

Untuk bintang, bintang dianggap berbentuk bola sempurna sehingga luas pemancar radiasinya (A) adalah 4πR² ; dengan R menyatakan radius bintang. Jadi, luminositas bintang (L) adalah :

L = 4πR² σT⁴ .......................... (pers. 4)

Benda hitam memancarkan radiasinya ke segala arah. Kita bisa menganggap pancaran radiasi tersebut menembus permukaan berbentuk bola dengan radius d dengan fluks energi yang sama, yaitu E. Besarnya E :

E = L/(4πd²) .......................... (pers. 5)

Fluks energi inilah yang diterima oleh pengamat dari bintang yang berada pada jarak d dari pengamat. Oleh karena itu, fluks energi ini sering disebut fluks energi yang diterima pengamat. (Warning : bedakan antara besaran E dan F).

Persamaan ini disebut juga hukum kuadrat kebalikan (invers square law) untuk kecerlangan (brightness, E) karena persamaan ini menyatakan bahwa kecerlangan (E) berbanding terbalik dengan kuadrat jaraknya (d). Jadi, makin jauh sebuah bintang, makin redup cahayanya.

Latihan:

1. Dari hasil pengukuran diperoleh bahwa permukaan seluas 1 cm² di luar atmosfer bumi menerima energi yang berasal dari Matahari sebesar 1,37 x 10⁶ erg/cm²/s. Apabila diketahui jarak Bumi-Matahari adalah 150 juta kilometer, tentukanlah luminositas Matahari.
2. Bumi menerima energi dari Matahari sebesar 1380 Watt/m². Berapakah energi dari Matahari yang diterima oleh planet Saturnus, jika jarak Matahari-Saturnus adalah 9,5 AU?
3. Luminositas sebuah bintang 100 kali lebih terang daripada Matahari, tetapi temperaturnya hanya setengahnya dari temperatur Matahari. Berapakah radius bintang tersebut dinyatakan dalam radius Matahari ?

(source : Dr. Djoni N. Dawanas)

Stars and Planets – 4th edition

Ian Ridpath has been adding to his impressive list of publications with the recently updated fourth edition of "Stars and Planets". Or, consider its more accurate and complete title "Princeton Field Guides Stars & Planets - The Most Complete Guide to the Stars, Planets, Galaxies and the Solar System". The title's quite a mouthful, but the book lives up to the billing. Within it, Ian Ridpath's texts and Wil Tirion's illustrations cover all that would interest an active, backyard astronomer.

Being the fourth edition, this review should assess changes from the book's predecessor. Lacking the third edition means I'm considering the book in isolation.

This book has two parts. The first includes star charts; four per month, with the northern latitude facing south and then north and the same for the southern latitude. The charts show about 5000 separate stars, all being a white dot on a pale blue background with black lettering. After this inclusion, there's notes on each of the 88 constellations. Again, star charts accompany each. To further entice the reader, nearly each constellation description has a wonderful, colour photograph of a particularly rewarding view, usually as seen from the National Optical Astronomy Observatory (NOAO) in Arizona.

However, as much as the NOAO facility is for the big league, this book stays true to being a guide for the amateur. As such, nearly all comments on viewing, and there are many, relate to either binoculars or small to mid-size home telescopes.

The second part of the book starts off with a look into the life cycle of stars and the particular and useful intricacies of the electromagnetic spectrum. Then, it proceeds to describe viewing pleasures on a planet by planet meander through our solar system. Further, twelve full page maps completely identify features shown on the Moon's near side. Again, the perspective is for that of a person using amateur level equipment. To help the reader along, the book concludes with a short discussion on choosing binoculars and telescopes.

Being a field guide, this book is of smaller stature than most. Yet, it still won't fit easily into most pant pockets. However, it would be a great asset to have on hand when deciding how to coordinate a star party or optimize personal evening viewing. And, though not stated in the title, it is for observers, so there's not a great depth of detail on why or what-for. Thus, for observers, it is of a just the right stature.

Though I'm not in a position to asses the title's proclamation of being the most complete guide, I will say that it is the best one that I've read. With Ian Ridpath's text and Wil Tirion's illustrations, the "Princeton Field Guides Stars & Planets" is a wonderful guide to the stars, planets, galaxies and our own solar system. It will help in getting that illusive target into the finder and onto the eagerly awaiting eye.

(Written by Mark Mortimer) and cited from: universetoday.com

Buku ini cocok digunakan khususnya oleh para astronom amatir, yang ingin mendapatkan panduan praktis dalam melakukan pengamatan. Buku ini menyertakan peta bintang, peta permukaan Bulan dan overview mengenai gelombang elektromagnetik dan tahapan evolusi bintang. Jika Anda tertarik membeli buku ini secara online, silakan klik link ini.

Angular diameter

After we talk about parallax, now we will discuss about angular diameter.

I. Definition

The angle that the actual diameter of an object makes in the sky; also known as angular size or apparent diameter. The angular diameter of an object as seen from a given position is the "visual diameter" of the object measured as an angle. The visual diameter is the diameter of the perspective projection of the object on a plane through its center that is perpendicular to the viewing direction. Because of foreshortening, it may be quite different from the actual physical diameter for an object that is seen under an angle. For a disk-shaped object at a large distance, the visual and actual diameters are the same.The Moon, with an actual diameter of 3,476 kilometers, has an angular diameter of 29' 21" to 33' 30", depending on its distance from Earth. If both angular diameter and distance are known, linear diameter can be easily calculated.

The Sun and the Moon have angular diameters of about half a degree, as would a 10-centimeter (4-inch) diameter orange at a distance of 11.6 meters (38 feet). People with keen eyesight can distinguish objects that are about an arc minute in diameter, equivalent to distinguishing between two objects the size of a penny at a distance of 70 meters (226 feet). Modern telescopes allow astronomers to routinely distinguish objects one arc second in diameter, and less. The Hubble Space Telescope, for example, can distinguish objects as small as 0.1 arc seconds. For comparison, 1 arc second is the apparent size of a penny seen at a distance of 4 kilometers (2.5 miles).

The angular diameter is proportional to the actual diameter divided by its distance. If any two of these quantities are known, the third can be determined.

For example if an object is observed to have an apparent diameter of 1 arc second and is known to be at a distance of 5,000 light years, it can be determined that the actual diameter is 0.02 light years.

II. Formulas

The angular diameter of an object can be calculated using the formula:

in which δ is the angular diameter, and d and D are the visual diameter of and the distance to the object, expressed in the same units. When D is much larger than d, δ may be approximated by the formula δ = d / D, in which the result is in radians.

For a spherical object whose actual diameter equals d_act, the angular diameter can be found with the formula:

for practical use, the distinction between d and d_act only makes a difference for spherical objects that are relatively close.

III. Estimating Angular Diameter

This illustration shows how you can use your hand to make rough estimates of angular sizes. At arm's length, your little finger is about 1 degree across, your fist is about 10 degrees across, etc. Credit: NASA/CXC/M.Weiss

IV. Use in Astronomy

In astronomy the sizes of objects in the sky are often given in terms of their angular diameter as seen from Earth, rather than their actual sizes.

The angular diameter of Earth's orbit around the Sun, from a distance of one parsec, is 2" (two arcseconds).

The angular diameter of the Sun, from a distance of one light-year, is 0.03", and that of the Earth 0.0003". The angular diameter 0.03" of the Sun given above is approximately the same as that of a person at a distance of the diameter of the Earth.[1]

This table shows the angular sizes of noteworthy celestial bodies as seen from the Earth:

Sun	31.6' – 32.7'
Moon	29.3′ – 34.1'
Venus	10″ – 66″
Jupiter	30″ – 49″
Saturn	15″ – 20″
Mars	4″ – 25″
Mercury	5″ – 13″
Uranus	3″ – 4″
Neptune	2″
Ceres	0.8″
Pluto	0.1″

* Betelgeuse: 0.049″ – 0.060″
* Alpha Centauri A: ca. 0.007″
* Sirius: ca. 0.007″

This meaning the angular diameter of the Sun is ca. 250,000 that of Sirius (it has twice the diameter and the distance is 500,000 times as much; the Sun is 10,000,000,000 times as bright, corresponding to an angular diameter ratio of 100,000, so Sirius is roughly 6 times as bright per unit solid angle).

The angular diameter of the Sun is also ca. 250,000 that of Alpha Centauri A (it has the same diameter and the distance is 250,000 times as much; the Sun is 40,000,000,000 times as bright, corresponding to an angular diameter ratio of 200,000, so Alpha Centauri A is a little brighter per unit solid angle).

The angular diameter of the Sun is about the same as that of the Moon (the diameter is 400 times as large and the distance also; the Sun is 200,000-500,000 times as bright as the full Moon (figures vary), corresponding to an angular diameter ratio of 450-700, so a celestial body with a diameter of 2.5-4" and the same brightness per unit solid angle would have the same brightness as the full Moon).

Even though Pluto is physically larger than Ceres, when viewed from Earth, e.g. through the Hubble Space Telescope, Ceres has a much larger apparent size.

While angular sizes measured in degrees are useful for larger patches of sky (in the constellation of Orion, for example, the three stars of the belt cover about 3 degrees of angular size), we need much finer units when talking about the angular size of galaxies, nebulae or other objects of the night sky.

Degrees, therefore, are subdivided as follows:

* 360 degrees (º) in a full circle
* 60 arc-minutes (′) in one degree
* 60 arc-seconds (′′) in one arc-minute

To put this in perspective, the full moon viewed from earth is about ½ degree, or 30 arc minutes (or 1800 arc-seconds). The moon's motion across the sky can be measured in angular size: approximately 15 degrees every hour, or 15 arc-seconds per second. A one-mile-long line painted on the face of the moon would appear to us to be about one arc-second in length.

Source : Wikipedia and encyclopedia of science.

Cited from : All About Astronomy

Parallax : Distance Measurement

Before we learn further about astronomy, there are some basic knowledges that we must know and understand.

First, we will talk about measuring distance in astronomy.

Astronomical object lies in a very great distance from us. So far than our sense can perceive. That's why our sense can't have a 3-D visualization of the universe. Our sense can't differ closer to farther objects. So, we need some trick to know how far an object from us. One of the simplest method used by astronomers to measure distance of some closest star is using the parallax effect.

Parallax is an optical effect seen when the observer seeing an object from two different positions. The object will be seen shifted relative to the farther background objects.

The parallax effect is one of those things you see everyday and think nothing of until it's given some mysterious scientific-sounding name. There's really no magic here. Consider the following simple situation.

You're riding in a car on a highway out west. It's a beautiful sunny day, and you can see for miles in every direction. Off to your left, in the distance, you see a snow-capped mountain. In front of that mountain, and much closer to the car, you see a lone ponderosa pine standing in a field next to the highway. I've diagramed this idyllic scene in the figure below:

As you drive by the field, you notice an interesting sight. When you're in the position on the left side of the figure, the tree appears to be to the right of the mountain. You can see this in the figure by the fact that the line of sight to the tree (indicated by the green line) is rightward of the line of sight to the mountain (indicated by the blue line). A picture of what you see out the window of your car is shown below the car.

The interesting part is that as your drive on, you notice that the tree and mountain have switched positions; that is, by the time you reach the right hand position in the above figure, the tree appears to be to the left of the mountain. You can see this in the figure by noting that the line of sight to the tree (green line) is leftward of the line of sight to the mountain (blue line). A picture of what you see out the window of your car now is shown below the car.

What's going on here? It's pretty clear that the tree and mountain haven't moved at all, yet the tree appears to have jumped from one side of the mountain to the other. By now, you're probably saying "Well, DUH, the tree is just closer to me than the mountain. What's so remarkable about that?" I would answer, "There's nothing at all remarkable about it. It's just the effect of parallax." In fact, if you understand the above discussion, you already understand the parallax effect.

Now let's talk about measuring the distance to the tree using this information. From the above information, you can see that it would be pretty easy to measure the angle between the direction to the tree and the direction to the mountain in both instances. Let's call those angles A and B, respectively. Now, if the mountain is sufficiently distant so that the direction to the mountain from both viewpoints is the same, then the two blue lines in the figure below are parallel.

This helps a lot, because we can then show that the angle made by the two green lines (i.e., the difference in the direction to the pine tree from the two viewpoints) is equal to the sum of A and B. To see this, construct a line through the pine tree parallel to the two blue lines in the figure (this line is shown as a dotted line above). Then all of the blue lines are parallel, and each of the green lines crosses a pair of parallel lines. Reach deep back into your high school geometry (or equivalently, just stare at the above figure for a minute), and you'll remember or realize that the angles at the pine tree labeled A and B have the same values as the angles A and B measured at the two car positions. Thus, the angle between the two green lines is the sum of A and B, which are angles we can measure from the comfort of our car.

Now, if we know the distance D we've traveled, then we have an Observer's Triangle and we can solve for the distance to the tree using the Observer's Triangle relation

alpha/57.3 = D/R where alpha is the angle at the tree (A + B), D is the distance we've traveled between views, and R is the distance from the road to the tree. (source : Astronomy 101 Specials: Measuring Distance via the Parallax Effect).

We will use the same method to measure the star's distance. This method is called trigonometric parallax because we only use simple triangulation to find the distance. The only problem is star's distance is so huge so the parallax effect will be so small (less than 1 arc second; 1 arc second = 1/3600 of a degree). So, that's why this method can only measure accurately for several nearby stars. Farther star will need different, more complex, indirect method to derive its distance.

As explained before, the stars are so far away that observing a star from opposite sides of the Earth would produce a parallax angle much, much too small to detect (That's why ancient people can't detect this shifting to prove heliocentric view) . As a consequence, we must use the largest possible baseline. The largest one that can be easily used is the orbit of the Earth. In this case the baseline is the mean distance between the Earth and the Sun---an astronomical unit (AU) or 149.6 million kilometers! A picture of a nearby star is taken against the background of stars from opposite sides of the Earth's orbit (six months apart). The parallax angle p is one-half of the total angular shift.

However, even with this large baseline, the distances to the stars in units of astronomical units are huge, so a more convenient unit of distance called a parsec is used (abbreviated with "pc''). A parsec is the distance of a star that has a parallax of one arc second using a baseline of 1 astronomical unit. Therefore, one parsec = 206,265 astronomical units. The nearest star is about 1.3 parsecs from the solar system. In order to convert parsecs into standard units like kilometers or meters, you must know the numerical value for the astronomical unit---it sets the scale for the rest of the universe. Its value was not know accurately until the early 20th century. In terms of light years, one parsec = 3.26 light years.

Using a parsec for the distance unit and an arc second for the angle, our simple angle formula above becomes extremely simple for measurements from Earth:

p = 1/d

Parallax angles as small as 1/50 arc second can be measured from the surface of the Earth. This means distances from the ground can be determined for stars that are up to 50 parsecs away. If a star is further away than that, its parallax angle p is too small to measure and you have to use more indirect methods to determine its distance. Stars are about a parsec apart from each other on average, so the method of trigonometric parallax works for just a few thousand nearby stars. The Hipparcos mission greatly extended the database of trigonometric parallax distances by getting above the blurring effect of the atmosphere. It measured the parallaxes of 118,000 stars to an astonishing precision of 1/1000 arc second (about 20 times better than from the ground)! It measured the parallaxes of 1 million other stars to a precision of about 1/20 arc seconds. Selecting the Hipparcos link will take you to the Hipparcos homepage and the catalogs.

The actual stellar parallax triangles are much longer and skinnier than the ones typically shown in astronomy textbooks. They are so long and skinny that you do not need to worry about which distance you actually determine: the distance between the Sun and the star or the distance between the Earth and the star. Taking a look at the skinny star parallax triangle above and realizing that the triangle should be over 4,500 times longer (!), you can see that it does not make any significant difference which distance you want to talk about. If Pluto's entire orbit was fit within a quarter (2.4 centimeters across), the nearest star would be 80 meters away! But if you are stubborn, consider these figures for the planet-Sun-star star parallax triangle setup above (where the planet-star side is the hypotenuse of the triangle):

the Sun -- nearest star distance = 267,068.230220 AU = 1.2948 pc

the Earth--nearest star distance = 267,068.230222 AU = 1.2948 pc

Pluto--nearest star distance = 267,068.233146 AU = 1.2948 pc!

If you are super-picky, then yes, there is a slight difference but no one would complain if you ignored the difference. For the more general case of parallaxes observed from any planet, the distance to the star in parsecs d = ab/p, where p is the parallax in arc seconds, and ab is the distance between the planet and the Sun in AU.

Formula (1) relates the planet-Sun baseline distance to the size of parallax measured. Formula (2) shows how the star-Sun distance d depends on the planet-Sun baseline and the parallax. In the case of Earth observations, the planet-Sun distance ab = 1 A.U. so d = 1/p. From Earth you simply flip the parallax angle over to get the distance! (Parallax of 1/2 arc seconds means a distance of 2 parsecs, parallax of 1/10 arc seconds means a distance of 10 parsecs, etc.)

A nice visualization of the parallax effect is the Distances to Nearby Stars and Their Motions lab (link will appear in a new window) created for the University of Washington's introductory astronomy course. With this java-based lab, you can adjust the inclination of the star to the planet orbit, change the distance to the star, change the size of the planet orbit, and even add in the effect of proper motion. (source : www.astronomynotes.com)

Units in Distance

1. Astronomical Unit (A.U). It is defined as the mean distance of the Sun from the Earth. Its value is about 149,6 million km. This unit is conveniently used to express distance to the object in solar system because we can directly compared the distance to Earth-Sun distance.


2. One light year is defined as the distance that light has traveled in light years. Light has velocity about 300.000 km/s. So, one light year equals to 9,46 x 10^12 km. This unit is mostly used to express the distance of extragalactic object. Remember that light's speed is finite so distant objects are seen as they are in the past. For example the Sun. The Sun that we see at this moment is the Sun as it was 8 minutes ago. Light needs about 8 minutes to travel the Earth-Sun distance. So, looking farther objects mean we're looking even further to the past. That's why light years is more commonly used to express distant object's distance. When we say that a cluster's distance is 8 billion light years, it means that the cluster that we seen right now is the way it looks 8 billion years ago !


3. Parsec (Parallax second). Star that have parallax 1 arc second have distance about 3,26 light years or 206.265 A.U (astronomical unit). Astronomer use this distance as a unit to express distance of the star. It is called a parsec. This unit is favorable to express star's distance because it is closely related to star's parallax (p). (remember that parallax = 1/distance, while the observer is on Earth, parallax is expressed in arc second and distance is expressed in parsec).

So, for reviewing our understanding about the parallax, try to answer these questions:

1. If a star has parallax 0",711, determine its distance (in light years) from us!


2. Assume we can measure parallax from Mars (with the same technology that we used here on Earth). Assume that we can measure accurately using parallax method until 200 parsec from the Earth (distance limit). Determine the distance limit if we conduct the measurement of star's distance using parallax method. Given that the distance of Mars from the Sun is about 1,52 AU.


3. You observe an asteroid approaching the Earth. You have two observatories 3200 km apart, so you can measure the parallax shift of the incoming asteroid. You observe the parallax shift to be 0,022 degrees.Determine : (a) the parallax expressed in radians (b) the asteroid's distance from Earth.


4. If you measure the parallax of a star to be 0,1 arc seconds on Earth, how big would the parallax of the same star for an observer on Mars?


5. If you measure the parallax of a star to be 0,5 arc seconds on Earth and an observer in a space station in the orbit around the Sun measures a parallax for the same star to be 1 arc seconds, how far is the space station from the Sun ?

You can share your solution of the above questions in the comment column.

(Source : all about astronomy)